Are you curious about the angles in a quadrilateral? Have you ever wondered how they are defined and what their properties are? In this article, we will explore the exciting world of quadrilateral angles, providing you with a solid understanding of their definitions and properties. Let's dive in!
What Are Angles in a Quadrilateral?
Angles in a quadrilateral are the four angles formed at each vertex. These angles are called the interior angles of a quadrilateral. If you draw a diagonal, you can see that a quadrilateral gets divided into two triangles. The sum of the interior angles of a triangle is 180°, so it follows that the sum of angles in a quadrilateral is 360°.
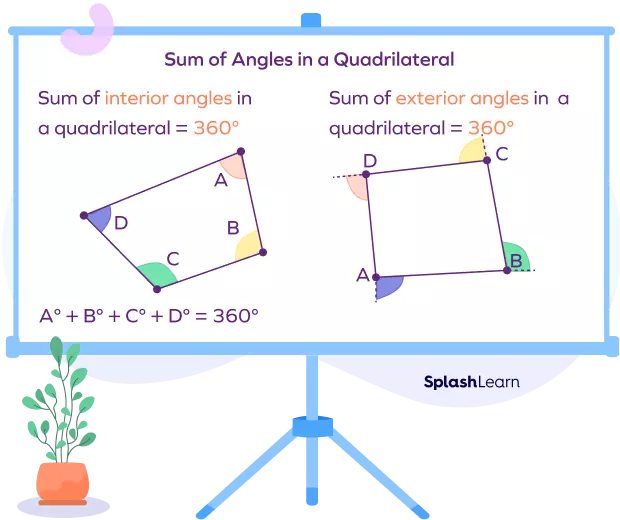Fig 1. Sum of angles in a quadrilateral is 360 degrees: visual proof
A quadrilateral is defined as a two-dimensional shape with four sides, four vertices, and four interior angles. It is a four-sided polygon formed by four non-collinear points.
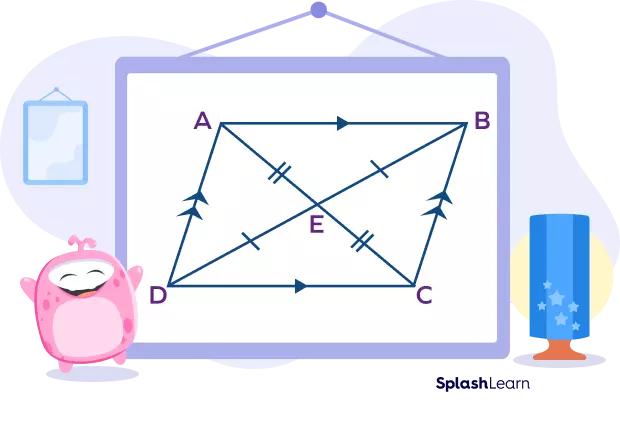
Fig 2. 4 non-collinear points forming a quadrilateral
In the figure above, ABCD is a quadrilateral. AB, BC, CD, and DA are its four sides, and A, B, C, and D are its four vertices. The four interior angles of this quadrilateral are angle A, angle B, angle C, and angle D.
Interior Angles and Exterior Angles of a Quadrilateral
A quadrilateral has 4 interior angles and 4 exterior angles. Let's understand the difference between these two types of angles.
Interior Angles of a Quadrilateral
The sum of the interior angles of a quadrilateral is always 360°. If there is a missing angle, we can use this property to find its measure.
Exterior Angles of a Quadrilateral
An exterior angle is formed by the intersection of any of the sides of a polygon and the extension of the adjacent side. The sum of all the exterior angles of a quadrilateral is also 360°.
Take a look at the quadrilateral ABCD. Angles 1, 2, 3, and 4 are the exterior angles, while angles A, B, C, and D are the interior angles.
Fig 3. Exterior angles of a quadrilateral is 180 degrees
We can observe that the sum of an interior angle and its corresponding exterior angle is always 180°.
Interior Angle + Corresponding Exterior Angle = 180°
angle A + angle 1 = 180°
angle B + angle 2 = 180°
angle C + angle 3 = 180°
angle D + angle 4 = 180°Angles of a Quadrilateral Formulas
Let's take a look at some basic formulas related to the interior and exterior angles of a quadrilateral.
Interior Angles Sum Property
The sum of the interior angles of a polygon can be calculated using the formula:
Sum = (n - 2) × 180°where "n" is the number of sides of the given polygon.
In a quadrilateral, n = 4, so the sum of the interior angles of a quadrilateral is (4 - 2) × 180° = 360°.
Note: If you know the measures of three angles of a quadrilateral, you can calculate the fourth angle using the formula: 360° - (Sum of the other 3 interior angles).
Interior angle and corresponding exterior angle
The sum of an interior angle and its corresponding exterior angle is always 180°.
- Exterior angle = 180° - Corresponding Interior angle
- Interior angle = 180° - Corresponding Exterior angle
Exterior Angles Sum of a Quadrilateral
The sum of the exterior angles of a quadrilateral is always 360°.
Let angles W, X, Y, Z be the exterior angles corresponding to the interior angles A, B, C, D of a quadrilateral respectively. Thus, W + X + Y + Z = (180° - A) + (180° - B) + (180° - C) + (180° - D) W + X + Y + Z = (180° + 180° + 180° + 180°) - (A + B + C + D) W + X + Y + Z = 720° - (A + B + C + D) W + X + Y + Z = 360°
Fig 4. Interior and exterior angles of a quadrilateral
How to Find the Missing Angle in a Quadrilateral
If you come across a quadrilateral with a missing angle, you can easily find it using the following steps:
Step 1: Use angle properties to determine the interior angles.
Step 2: Add all the known interior angles.
Step 3: Subtract the sum of the angles from 360° to find the missing angle.
Let's consider an example to illustrate this:
Example: Find the missing angle in the quadrilateral given below.
We know that the sum of the interior angles of a quadrilateral is 360°. Adding the given 3 angles, we get:
100° + 95° + 60° = 255°Subtracting the sum from 360°, we get:
360° - 255° = 105°Thus, the missing angle in the quadrilateral is 105°.
Properties of Angles in a Quadrilateral
Let us now explore the angle properties of some common quadrilaterals.
Rectangle
- All interior angles measure 90°.
- The diagonals bisect each other and form four angles at the point of intersection: two acute angles and two obtuse angles.
- The diagonals do not bisect the angles at the vertices.
- Vertically opposite angles are formed at the intersection of the diagonals.
Parallelogram
- Opposite angles are equal.
- Adjacent angles or consecutive angles are supplementary.
- Vertically opposite angles are formed at the intersection of the diagonals.
Square
- All interior angles are congruent and measure 90°.
- The diagonals bisect each other at right angles.
Rhombus
- Opposite angles are equal.
- Adjacent angles are supplementary.
- Diagonals of a rhombus bisect each other at right angles.
- Diagonals of a rhombus bisect vertex angles.
Quadrilateral Family
Take a look at the different types of quadrilaterals shown below. You can make an anchor chart to explore the different properties of angles and sides in each of the given quadrilaterals and their types. Give it a try!
Angles of a Quadrilateral Inscribed in a Circle
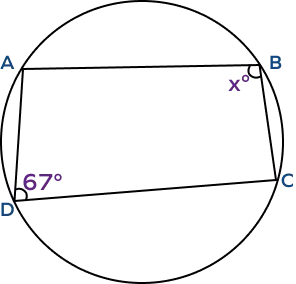
When a quadrilateral is inscribed in a circle, it is known as a cyclic quadrilateral or a chordal quadrilateral. It has all four vertices lying on the circumference of a circle, and the four sides of the quadrilateral form the chords of the circle.
The sum of opposite angles in a cyclic quadrilateral is 180°. In other words, opposite angles in a cyclic quadrilateral are supplementary.
Facts about Angles in a Quadrilateral
Here are some important facts to remember about angles in a quadrilateral:
- The sum of the interior angles of a quadrilateral is always 360°.
- Opposite angles in a cyclic quadrilateral are supplementary (i.e., they add up to 180°).
- The exterior angles of a quadrilateral sum up to 360°.
- Many different quadrilaterals have unique angle properties, such as rectangles, parallelograms, squares, and rhombuses.
Conclusion
In this article, we explored the angles of a quadrilateral, their properties, interior and exterior angles, angles of a quadrilateral inscribed in a circle, and some important formulas. Armed with this knowledge, you can confidently tackle problems involving quadrilateral angles. Go ahead and apply these formulas to solve some examples!
Practice Problems on Angles in a Quadrilateral
Here are a few practice problems for you to test your understanding of angles in a quadrilateral:
- The angles of a quadrilateral are in the ratio of 1 : 2 : 3 : 4. Find the measure of each angle.
- Find the exterior angle of a quadrilateral whose corresponding interior angle is 60°.
- Find the corresponding interior angle of a quadrilateral if its exterior angle is 104°.
- ABCD is a cyclic quadrilateral with center O. Find x.
Frequently Asked Questions on Angles in a Quadrilateral
Q: Why is the sum of interior angles of a quadrilateral always 360°? A: When a diagonal is drawn in a quadrilateral, it divides the shape into two triangles. The sum of the interior angles of a triangle is 180°, so the sum of the interior angles of two triangles is 360°.
Q: Do all quadrilaterals have the same angle properties? A: No, different types of quadrilaterals have unique angle properties. Rectangles, parallelograms, squares, and rhombuses are some examples of quadrilaterals with distinct angle properties.
Q: What are cyclic quadrilaterals? A: Cyclic quadrilaterals are quadrilaterals whose vertices lie on the circumference of a circle. They have interesting properties related to their opposite angles.
Q: How can I calculate a missing angle in a quadrilateral? A: To find a missing angle in a quadrilateral, use the fact that the sum of the interior angles is 360°. By subtracting the sum of the known angles from 360°, you can determine the measure of the missing angle.
Now that you have a solid understanding of angles in a quadrilateral, you can confidently tackle problems and explore the fascinating properties of these geometric shapes. Go ahead and put your knowledge into practice!
