Have you ever wondered about the mystical world of polygon angles? Well, get ready to have your mind blown as we delve into the intriguing realm of geometric shapes and their angles. In this article, we'll explore the sum of interior angles and the sum of exterior angles of polygons. Get ready to unlock the secrets of polygons!
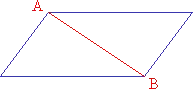Image: Interior and Exterior Angles of a Polygon
Unveiling the Sum of Interior Angles
Let's start by unraveling the mysteries of the sum of interior angles in a polygon. We'll begin with the simplest of them all, the triangle. You probably already know that the sum of interior angles in a triangle is always 180°. This is known as the Triangle Sum Theorem.
But what about other polygons? Fear not, we have a foolproof method to find the sum of interior angles for any polygon. Simply divide the polygon into triangles by drawing diagonals from a single vertex. Take a look at the quadrilateral below, for example. By drawing a diagonal from vertex A to vertex B, we separate the quadrilateral into two triangles.
Image: Quadrilateral Divided into Triangles
Since we know that the sum of angles in a triangle is 180°, we can conclude that the sum of interior angles in a quadrilateral is 180° × 2 = 360°. Similarly, a pentagon can be divided into three triangles, resulting in a sum of interior angles of 180° × 3 = 540°. A hexagon can be divided into four triangles, giving us a sum of interior angles of 180° × 4 = 720°.
The Formula for the Sum of Interior Angles
Based on the patterns we observed, we can generalize the formula for finding the sum of interior angles in any polygon. The number of triangles in a polygon is always two less than the number of sides. Therefore, we can use the formula (n - 2) × 180°, where n represents the number of sides of the polygon.
Image: Formula for the Sum of Interior Angles
Let's put this formula to the test with some examples. For a heptagon (7-sided polygon), the formula becomes (7 - 2) × 180° = 5 × 180° = 900°. Therefore, the sum of the interior angles of a heptagon is 900°. Now, let's consider a regular octagon (8-sided polygon). Using the same formula, each interior angle of an octagon is 135°.
Exploring the Sum of Exterior Angles
Now that we've unravelled the secrets of interior angles, it's time to shift our focus to the sum of exterior angles. Brace yourself, because this is where it gets even more fascinating! Did you know that the sum of exterior angles of any polygon is always 360°? It's a mind-boggling fact that applies to all polygons, regardless of the number of sides.
For a regular n-sided polygon, each exterior angle measures 360°/n. This means that the exterior angles become smaller as the number of sides increases. Take a moment to ponder this intriguing phenomenon!
Delving Deeper with Practical Examples
To solidify your understanding of polygon angles, let's explore a few practical examples. We'll determine the measure of each exterior and interior angle of a regular polygon, as well as solve a problem involving the sum of exterior angles.
For more in-depth explanations and step-by-step solutions, check out the video lessons provided. They offer a comprehensive guide to mastering polygon angles and will surely satisfy your thirst for geometric knowledge.
Join the Fascination of Polygon Angles
Congratulations! You've embarked on a fascinating journey through the captivating world of polygon angles. From the sum of interior angles to the intriguing patterns of exterior angles, you've witnessed the beauty of geometry in action.
If you're hungry for more mathematical adventures or have any questions, feel free to explore our website or reach out to us. We're here to guide you and satisfy your curiosity. So, embrace your inner math enthusiast and continue to unravel the mysteries of the mathematical universe!
Note: The images used in this article are property of the original source and are provided for visual representation purposes.
