Have you ever wondered about the intriguing angles of a quadrilateral? These four-sided polygons hold a secret - their interior angles always add up to a mesmerizing 360°. From squares to rectangles, rhombuses, and more, quadrilaterals come in various forms, each with its own set of angles waiting to be discovered. Let's dive into the world of quadrilateral angles and uncover the mysteries they hold.
The Sum of Interior Angles
It's a fascinating fact - a quadrilateral has four interior angles, and their sum always amounts to 360°. This remarkable value is derived from the angle sum property of polygons. If we consider the number of triangles that can be formed within a polygon by drawing diagonals from a single vertex, we can calculate the sum of its interior angles. A handy formula comes to our rescue, stating that for a polygon with 'n' sides, the sum of its interior angles is given by (n - 2) × 180°.
Let's take a quadrilateral with four sides as an example. Applying the formula, we find that the sum of its interior angles is (4 - 2) × 180° = 2 × 180° = 360°. Hence, according to the angle sum property of a quadrilateral, the total of its interior angles is always a perfect 360°. This property comes in handy when we need to find the value of an unknown angle, given the knowledge of other angles. Simply subtract the sum of the known angles from 360°, and voila, the mystery is solved!
Exploring Interior and Exterior Angles
Within a quadrilateral, we find not only interior angles but also exterior angles. The interior angles lie inside the quadrilateral, while the exterior angles are formed between one side of the quadrilateral and another line extended from an adjacent side. Notably, each interior angle and its corresponding exterior angle form a linear pair.
For squares and rectangles, the interior angles are all right angles, measuring 90° each. As for other quadrilaterals, their interior angles may vary, adding to the excitement of discovery.
Formulas for Quadrilateral Angles
To delve deeper into the world of quadrilateral angles, let's explore some essential formulas:
-
Exterior angle = 180° - Interior angle: This formula helps find the value of the corresponding exterior angle when the interior angle is known. It can also be used in reverse to find the interior angle when the exterior angle is given.
-
If three angles of a quadrilateral are known, the fourth angle can be calculated using the formula: 360 - (Sum of the other 3 interior angles).
-
The sum of interior angles of a quadrilateral is represented by the formula: Sum = (n − 2) × 180°, where 'n' represents the number of sides of the quadrilateral. For a quadrilateral, with 'n' equal to 4, the sum is calculated as (4 − 2) × 180° = 360°.
The Enigma of Cyclic Quadrilaterals
When a quadrilateral is inscribed in a circle, it becomes a mesmerizing cyclic quadrilateral. All four vertices of the quadrilateral touch the circle, creating a mystical connection. Many theorems are associated with the angles of quadrilaterals inscribed in a circle. One such theorem states that the opposite angles in a cyclic quadrilateral are supplementary, meaning their sum is equal to 180°.
Let's take a moment to admire the beauty of a cyclic quadrilateral and observe how its opposite angles elegantly add up to 180°.
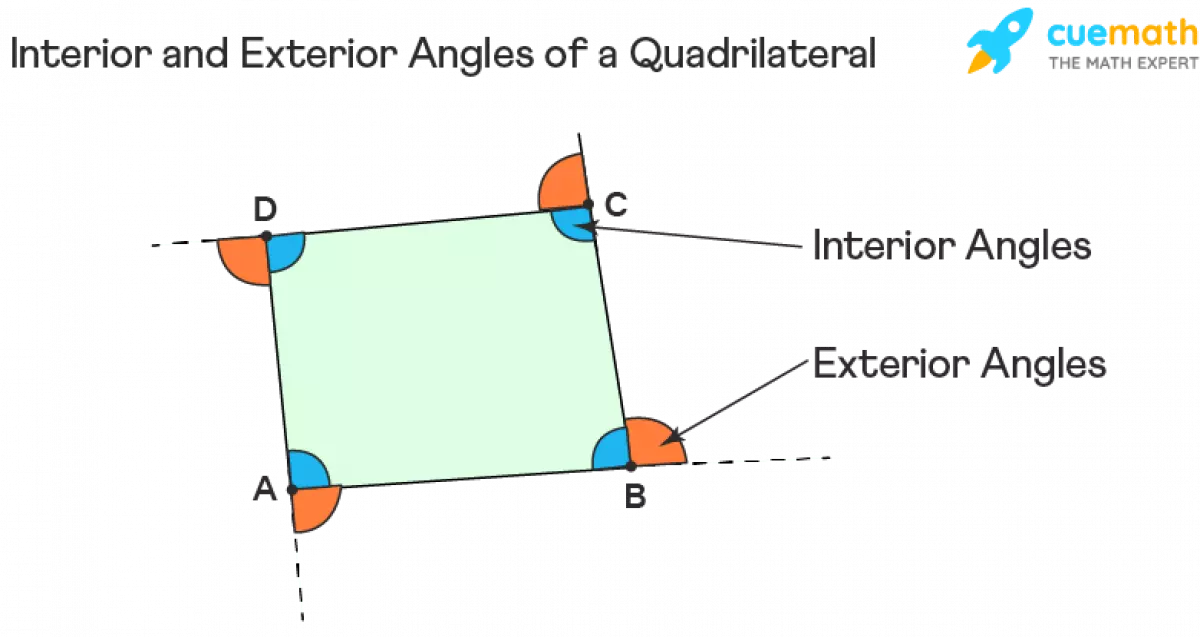Caption: Interior and Exterior Angles of a Quadrilateral
In the Quest for Knowledge
If you're hungry for more knowledge about quadrilateral angles, here are some related links to explore:
- Interior Angles
- Quadrilaterals
- Exterior Angles of Polygons
The world of quadrilateral angles is truly captivating. Knowing the secrets of interior and exterior angles and the formulas that unlock their mysteries allows us to navigate the enchanting realm of quadrilaterals with confidence. So, go forth and embrace the magic of quadrilateral angles!
