Introduction
Have you ever wondered about the exterior angles of a polygon? These angles define the shape and structure of a polygon, and their properties never cease to amaze mathematicians. In this article, we will explore the concept of exterior angles in detail and unravel their secrets.
What are Exterior Angles?
An exterior angle of a polygon is formed by one side of the shape and the extension of its adjacent side. It lies on the outside of the polygon, as shown in the figure below.
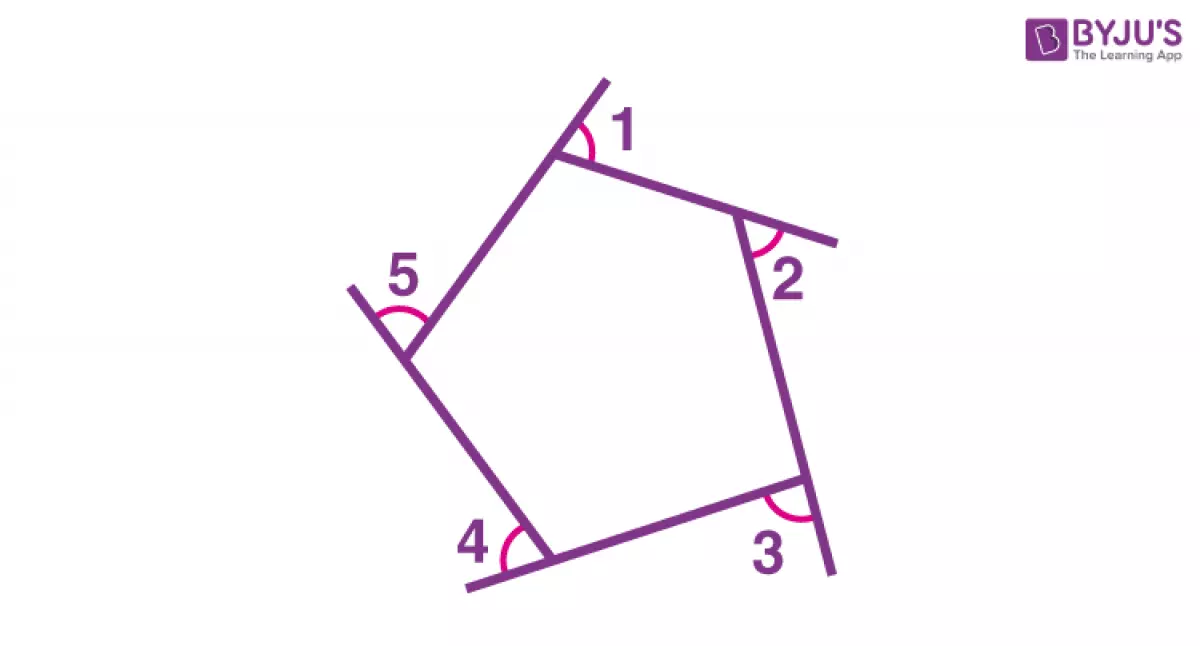 The exterior angles of a pentagon
The exterior angles of a pentagon
Here are a few key points about exterior angles:
- The sum of an interior angle and its corresponding exterior angle is always 180 degrees, as they lie on the same straight line.
- In the figure, angles 1, 2, 3, 4, and 5 are the exterior angles of the polygon.
- Fun Fact: Exterior angles of a regular polygon are equal in measure.
Sum of the Exterior Angles of a Polygon
Let's embark on a journey around the perimeter of a polygon, starting from vertex angle 1. As we travel clockwise, making turns through angles 2, 3, 4, and 5, we eventually return to the same vertex. In this process, we cover the entire perimeter of the polygon, completing one full turn. And do you know how much a full turn is? It's 360 degrees!
Hence, it can be concluded that angles 1, 2, 3, 4, and 5 add up to 360 degrees. In other words, the sum of the measures of the exterior angles in any polygon is always 360 degrees, regardless of the number of sides it has.
Polygon Exterior Angle Sum Theorem
If a polygon is convex, meaning all its interior angles are less than 180 degrees, then the sum of its exterior angles (one at each vertex) will always be equal to 360 degrees. Let's prove this theorem:
Proof: Consider an n-gon, a polygon with n sides. The sum of its exterior angles is denoted as N.
For any closed structure formed by sides and vertices, the sum of the exterior angles is always equal to the sum of linear pairs and the sum of interior angles. Therefore, N = 180n - 180(n-2) N = 180n - 180n + 360 N = 360
Hence, we have proven that the sum of the exterior angles of an n-gon is always 360 degrees.
Video Lesson on Angle Sum and Exterior Angle Property
To further enhance your understanding, watch this enjoyable video lesson on the angle sum and exterior angle property.
Exterior Angles Examples
Let's explore a couple of examples to solidify our knowledge of exterior angles.
Example 1: Finding the Value of x In the given figure, we need to find the value of angle x.
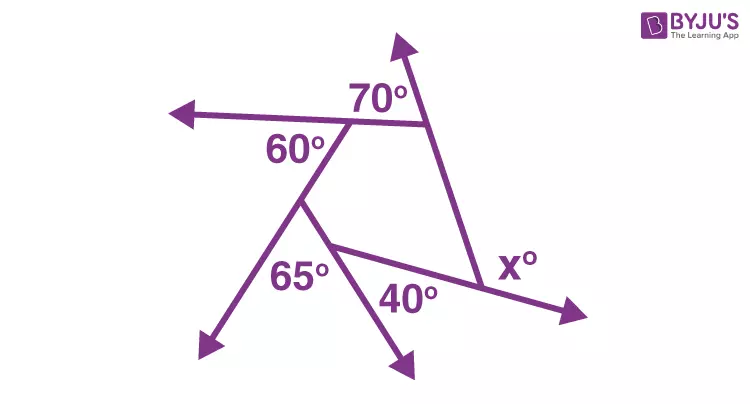
Solution: We know that the sum of the exterior angles of a polygon is 360 degrees. Hence, 70° + 60° + 65° + 40° + x = 360° 235° + x = 360° x = 360° - 235° = 125°
Example 2: Identifying the Type of Regular Polygon Given that the exterior angle of a regular polygon measures 120 degrees, let's determine the type of polygon.
Solution: Since the polygon is regular, all its interior angles have the same measure. Therefore, the exterior angles also have the same measure, which is 120 degrees. Knowing that the sum of exterior angles is 360 degrees, and each angle measures 120 degrees, we can conclude: Number of angles = 360/120 = 3 Since the polygon has 3 exterior angles, it has 3 sides. Hence, it is an equilateral triangle.
Now that you are acquainted with the intriguing world of exterior angles in polygons, you can explore more about polygons and their properties.


















