In the realm of geometry, interior angles hold a significant place. They are not just angles that lie inside a shape, but they also play a crucial role in understanding the measurements and properties of various polygons. Let's dive deep into the world of interior angles and explore their types and applications.
What are Interior Angles?
Interior angles can be defined in two ways: angles inside a polygon and angles formed when parallel lines are intersected by a transversal. Let's take a closer look at both types.
Angles inside a Polygon:
When we consider angles inside a shape, typically a polygon, we refer to them as interior angles. In the figure below, angles ∠a, ∠b, and ∠c are some examples of interior angles.
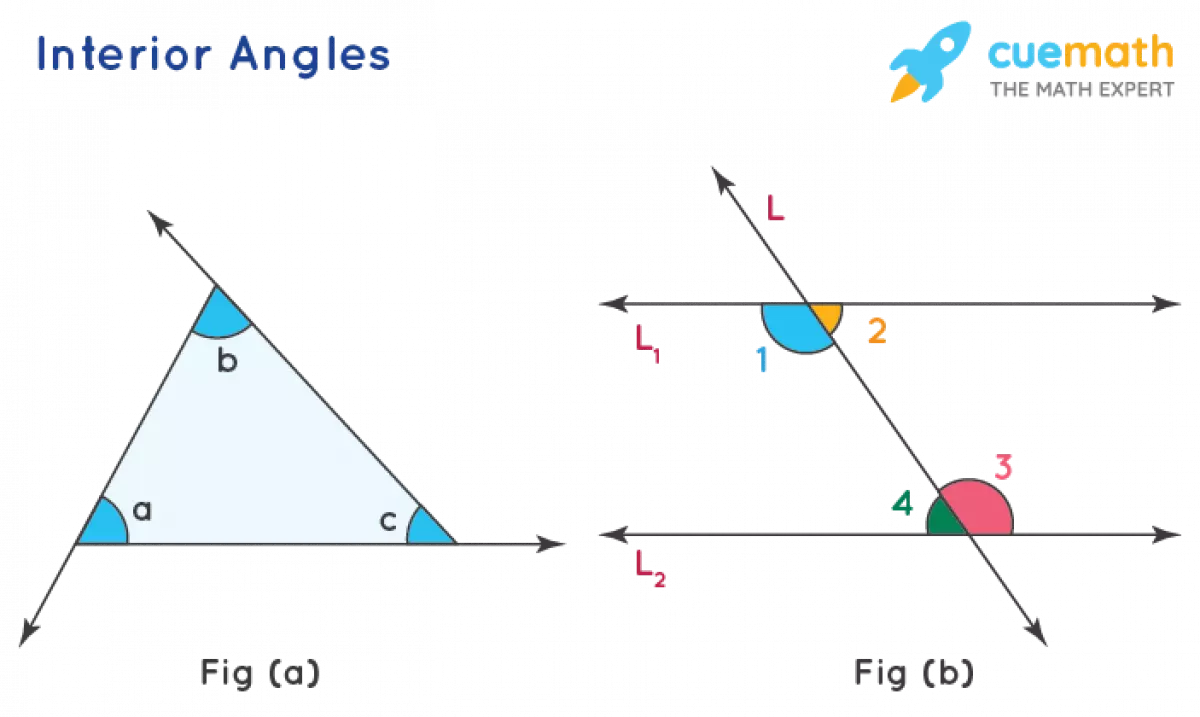Interior Angles
Interior Angles of Parallel Lines:
Another way interior angles are formed is when two parallel lines are intersected by a transversal. In the figure below, (L₁) and (L₂) are parallel lines intersected by the transversal, L. The angles ∠1, ∠2, ∠3, and ∠4 are examples of interior angles.
Interior Angles
Types of Interior Angles:
Within the realm of interior angles, two types are particularly significant: alternate interior angles and co-interior angles.
Alternate Interior Angles:
When two parallel lines are intersected by a transversal, alternate interior angles are formed. These angles are non-adjacent and located on opposite sides of the transversal. In the figure above, the pairs of alternate interior angles are ∠1 and ∠3, ∠2 and ∠4. An interesting property of alternate interior angles is that they are equal in measurement when two parallel lines are intersected by a transversal.
Co-Interior Angles:
Co-interior angles, also known as same-side interior angles or consecutive interior angles, are pairs of non-adjacent interior angles on the same side of the transversal. In the figure above, the pairs of co-interior angles are ∠1 and ∠4, ∠2 and ∠3. The sum of two co-interior angles is always 180°, making them a pair of supplementary angles.
Interior Angles in Polygons:
Interior angles in polygons play a crucial role in understanding the properties and measurements of polygons. In any polygon, the sum of the interior angles is always 180°. This property allows us to derive a formula to calculate the sum of interior angles in any polygon:
Sum, S = (n - 2) × 180°
Here, S represents the sum of the interior angles and n represents the number of sides of the polygon. Let's apply this formula to a triangle:
S = (3 - 2) × 180° = 180°
Using the same formula, we can calculate the sum of interior angles in other polygons:
| Polygon | Number of Sides, n | Sum of Interior Angles, S |
|---|---|---|
| Triangle | 3 | 180° |
| Quadrilateral | 4 | 360° |
| Pentagon | 5 | 540° |
| Hexagon | 6 | 720° |
| Heptagon | 7 | 900° |
| Octagon | 8 | 1080° |
| Nonagon | 9 | 1260° |
| Decagon | 10 | 1440° |
Finding an Unknown Interior Angle:
The "Sum of Interior Angles Formula" allows us to find unknown interior angles in polygons. Let's consider an example to find the missing angle (∠x) in the hexagon below:
From the table of interior angles in polygons, we know that the sum of interior angles in a hexagon is 720°. Two of the interior angles in the above hexagon are right angles. Therefore, we can set up the following equation:
90 + 90 + 140 + 150 + 130 + x = 720°
Simplifying the equation, we find:
600 + x = 720
x = 720 - 600 = 120
Thus, the missing interior angle (∠x) is 120°.
Understanding Regular Polygons:
A regular polygon is one in which all sides and angles are congruent. Each interior angle in a regular polygon can be calculated by dividing the sum of the angles by the number of sides. The formula for finding each interior angle in a regular polygon is:
Each Interior Angle = ((180(n - 2)) / n)°
Let's apply this formula to find the interior angle of a regular pentagon. A pentagon has 5 sides (n = 5):
((180(n - 2)) / n)° = ((180(5 - 2)) / 5)° = (180 × 3) / 5 = 540 / 5 = 108°
Thus, each interior angle of a regular pentagon is 108°.
Using the same formula, we can calculate the interior angles of other regular polygons:
| Regular Polygon | Sum of Interior Angles, S | Measurement of Each Interior Angle |
|---|---|---|
| Triangle | 180° | 60° (n = 3) |
| Square | 360° | 90° (n = 4) |
| Pentagon | 540° | 108° (n = 5) |
| Hexagon | 720° | 120° (n = 6) |
| Heptagon | 900° | 128.57° (n = 7) |
| Octagon | 1080° | 135° (n = 8) |
| Nonagon | 1260° | 140° (n = 9) |
| Decagon | 1440° | 144° (n = 10) |
Related Articles on Interior Angles:
If you're interested in exploring more about interior angles, check out the following related articles:
- Vertical Angles
- Alternate Angles
- Alternate Exterior Angles
- Same Side Interior Angles
- Interior Angles of Polygon Calculator
Important Notes:
Here are a few key points to remember when studying interior angles:
- The sum of the interior angles of a polygon with 'n' sides can be calculated using the formula 180(n - 2)°.
- Each interior angle of a regular polygon with 'n' sides can be calculated using the formula ((180(n - 2)) / n)°.
- As per the alternate interior angles theorem, when a transversal intersects two parallel lines, each pair of alternate interior angles are equal. Conversely, if a transversal intersects two lines such that a pair of interior angles are equal, then the two lines are parallel.
- As per the co-interior angles theorem, if a transversal intersects two parallel lines, each pair of co-interior angles is supplementary (their sum is 180°). Conversely, if a transversal intersects two lines such that a pair of co-interior angles are supplementary, then the two lines are parallel.
