Geometry can sometimes feel like an intimidating subject, but it doesn't have to be. In this article, we'll take a closer look at interior angles, their definitions, types, and formulas, and make them more accessible and understandable. So let's dive in!
What Are Interior Angles?
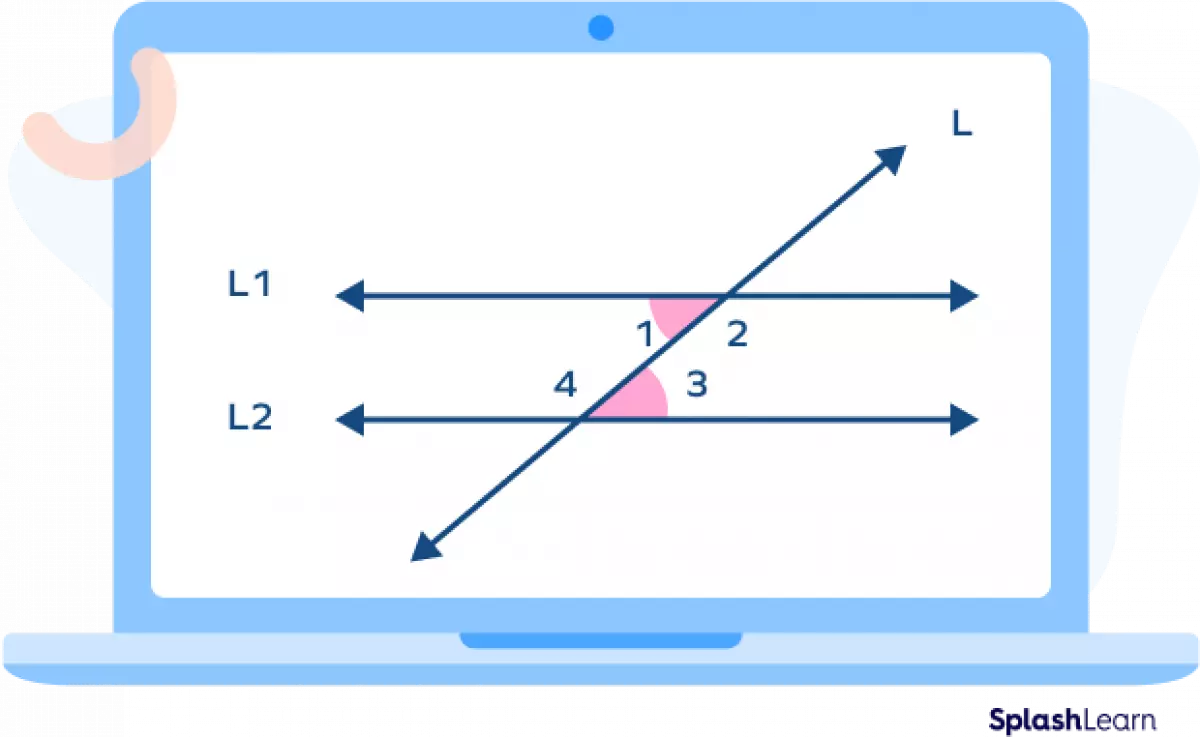
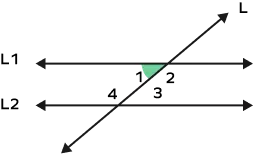
In geometry, the term "interior angles" can be used in two different contexts. Firstly, when two parallel lines are cut by a transversal, interior angles are formed. Secondly, interior angles are the angles that lie inside a polygon, a shape formed by sides.
Understanding the Types of Interior Angles
When a transversal cuts two parallel lines, two types of interior angles are formed: same-side interior angles and alternate interior angles.
Same-Side Interior Angles (Co-interior Angles)
These are pairs of non-adjacent angles that lie on the same side of the transversal. The sum of two co-interior angles is always 180°, making them supplementary.
Alternate Interior Angles
Alternate interior angles lie on the opposite sides of the transversal. The Alternate Interior Angles Theorem states that if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.
Exploring Interior Angles in Polygons
Interior angles also play a significant role in polygons. They are the angles that lie inside a polygon, formed by its sides.
Types of Triangles Based on Interior Angles
The interior angles of a triangle are crucial in classifying triangles into different categories:
- Acute Triangle: A triangle with all three interior angles as acute.
- Obtuse Triangle: A triangle with one interior angle as obtuse and the other two angles as acute.
- Right Triangle: A triangle with one interior angle as a right angle and the other two angles as acute.
Calculating Interior Angles: Sum and Unknown Angles
To calculate the sum of interior angles of any polygon, including a triangle, we can use the formula:
Sum of interior angles = (n - 2) × 180°
For example, a triangle has three interior angles, so the sum of its interior angles is always 180°. Similarly, we can calculate the sum of interior angles for polygons with any number of sides.
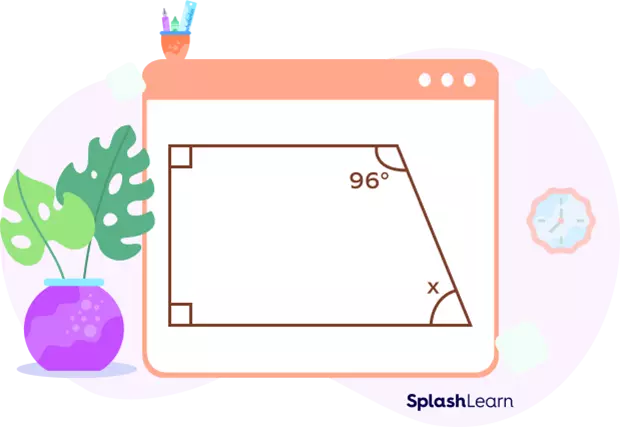
Finding Unknown Interior Angles and Regular Polygons
Using the sum of interior angles formula, we can also find unknown interior angles of polygons. For example, we can determine the value of a missing angle in a quadrilateral or the measure of each interior angle in a regular polygon.
Interesting Facts and Concluding Thoughts
- The sum of the interior angles of a polygon is always equal to the product of (n - 2) and 180°, where n represents the number of sides.
- In a regular polygon, all the interior angles are congruent.
- Interior angles are essential for understanding and solving geometry problems.
In conclusion, interior angles are a fundamental concept in geometry that helps us understand and solve various problems. By knowing their types, formulas, and properties, we can navigate the world of shapes and polygons with confidence.
I hope this article has shed light on the fascinating world of interior angles and made them more approachable. Now you're ready to tackle geometry problems like a pro!
References
- Image Source 1: Interior angles formed by a transversal cutting two parallel lines
- Image Source 2: Interior angles of a polygon
- Image Source 3: Regular polygons examples









