Are you intrigued by geometric shapes that possess a captivating allure? Look no further than the nonagon - a polygon consisting of nine sides, nine interior angles, and nine exterior angles. In this article, we will delve into the fascinating world of nonagons and explore their unique properties.
What Makes a Nonagon?
A nonagon is a versatile figure that can take on different forms, such as regular or irregular, convex or concave. Its name derives from the Latin words 'nonus' and 'gon,' which means a polygon with nine sides. Let's take a moment to appreciate the beauty of this shape:
Nonagon - a polygon with 9 sides
As you can see, a nonagon can have sides of equal or varying lengths, depending on its type.
Unveiling the Regular Nonagon
One particular form of the nonagon is the regular nonagon. In this configuration, all nine sides are of equal length, and the nine interior angles are congruent. On the other hand, an irregular nonagon features sides of different lengths and angles of varying measures.
The Fascinating Properties of a Regular Nonagon
Let's explore some noteworthy characteristics of a regular nonagon:
- All the sides of a regular nonagon are of equal length, ensuring geometric harmony.
- The sum of the interior angles of a regular nonagon is a remarkable 1260°, while the sum of the exterior angles amounts to 360°.
- Each interior angle of a regular nonagon measures an intriguing 140°.
To further illustrate the distinction between a regular nonagon and its irregular counterpart, take a look at this visual representation:
Regular Nonagon and Irregular Nonagon
Exploring Convex and Concave Nonagons
Within the realm of nonagons, we encounter two fascinating variations: convex and concave nonagons. Let's uncover their unique characteristics:
Convex Nonagon: Delicate Elegance
A convex nonagon mesmerizes us with its delicate elegance. Here's what you need to know about this configuration:
- All the interior angles of a convex nonagon measure less than 180°.
- The seemingly outward-bulging appearance of convex nonagons is a result of their interior angles being less than 180°.
Concave Nonagon: Intriguing Curves
Concave nonagons possess their own alluring charm. Discover their captivating traits:
- At least one interior angle of a concave nonagon forms a reflex angle.
- The vertices of a concave nonagon create a captivating inward curvature, which sets it apart from other polygon shapes.
Take a moment to marvel at these visual representations of convex and concave nonagons:
Convex Nonagon and Concave Nonagon
The Enigmatic Angles of a Nonagon
Now, let's turn our attention to the angles found within a nonagon. A nonagon boasts nine interior angles and nine corresponding exterior angles. Let's explore their intriguing characteristics:
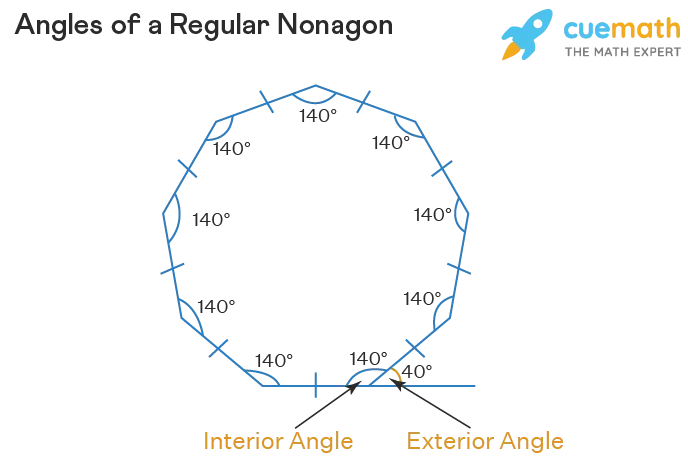
Angles of a Regular Nonagon
Interior Angles of a Nonagon
The measurements of the interior angles of a regular nonagon are a mesmerizing 140° each. To calculate this value, we use the formula for regular polygon interior angles:
Interior angle of a regular polygon = (180n - 360) / nFor a nonagon, with n being 9, we substitute this value into the formula, resulting in an interior angle of 140°.
The sum of the interior angles of any nonagon, regardless of its type, always totals 1260°. This can be determined using the formula:
Sum of interior angles of a polygon = (n - 2) × 180°By substituting n = 9 into the formula, we find that the sum of the interior angles of a nonagon is 1260°.
Exterior Angles of a Nonagon
Each exterior angle of a regular nonagon measures 40°. In the visual representation mentioned earlier, you can observe that the interior and exterior angles form linear pairs, totaling 180°. Therefore, the exterior angle of a regular nonagon is calculated as follows: 180° - 140° = 40°. The sum of the exterior angles of a nonagon is 360°.
Unveiling More Nonagon Properties
Let's discover additional properties that distinguish the nonagon from other polygons:
- A nonagon possesses the captivating combination of nine sides, nine interior angles, and nine exterior angles.
- The intriguing sum of the nonagon's interior angles always amounts to 1260°.
- A nonagon showcases a stunning network of 27 diagonals that connect its non-adjacent vertices.
Embracing the Nonagon's Diagonals
The nonagon mesmerizes us once more with its intricate network of diagonals. With a total of 27 diagonals, the nonagon offers a captivating exploration of its interior. We can calculate the number of diagonals in a nonagon using the following formula:
Number of diagonals in a polygon = 1/2 × n × (n-3)By substituting n = 9 into the formula, we find that a nonagon possesses 27 diagonals.
Enjoying the Perimeter of a Nonagon
The perimeter of a polygon represents the total length of its boundary. To determine the perimeter of a nonagon, we need to know the lengths of all nine sides. By summing up the lengths of all sides, we arrive at the perimeter. In the case of a regular nonagon, where all sides are of equal length, we can multiply the length of one side by 9 to calculate the perimeter. The formulas can be expressed as follows:
- Perimeter of a nonagon: Sum of all its sides.
- Perimeter of a regular nonagon: 9a (where 'a' represents the length of one side of the nonagon).
Now you have embarked on a captivating journey into the world of the nonagon. Its enigmatic angles, mesmerizing diagonals, and distinctive properties have left us in awe. So, next time you encounter this intricate polygon, take a moment to appreciate its allure.
☛ Related Articles
- Types of Polygon
- Pentagon
- Hexagon
- Heptagon
- Octagon
- Decagon
- Dodecagon
- Dodecahedron
