In the realm of geometry, there exists a shape that is both mesmerizing and versatile - the octagon. With its eight sides and eight angles, the octagon holds a special place in the world of polygons. Let's dive into the captivating world of octagons and explore their intriguing properties.
Unveiling the Octagon
The octagon, derived from the Greek word "oktágōnon" meaning "eight angles," is a polygon with eight sides. A regular octagon is a particular type of octagon with all sides and angles equal. It can be represented by the Schläfli symbol {8} [1]. However, an octagon can also take the form of a quasiregular truncated square, denoted as t{4}, with alternating types of edges.
Exploring the Properties
The octagon harbors fascinating properties that captivate mathematicians and enthusiasts alike. Here are some notable ones:
Angles and Symmetry
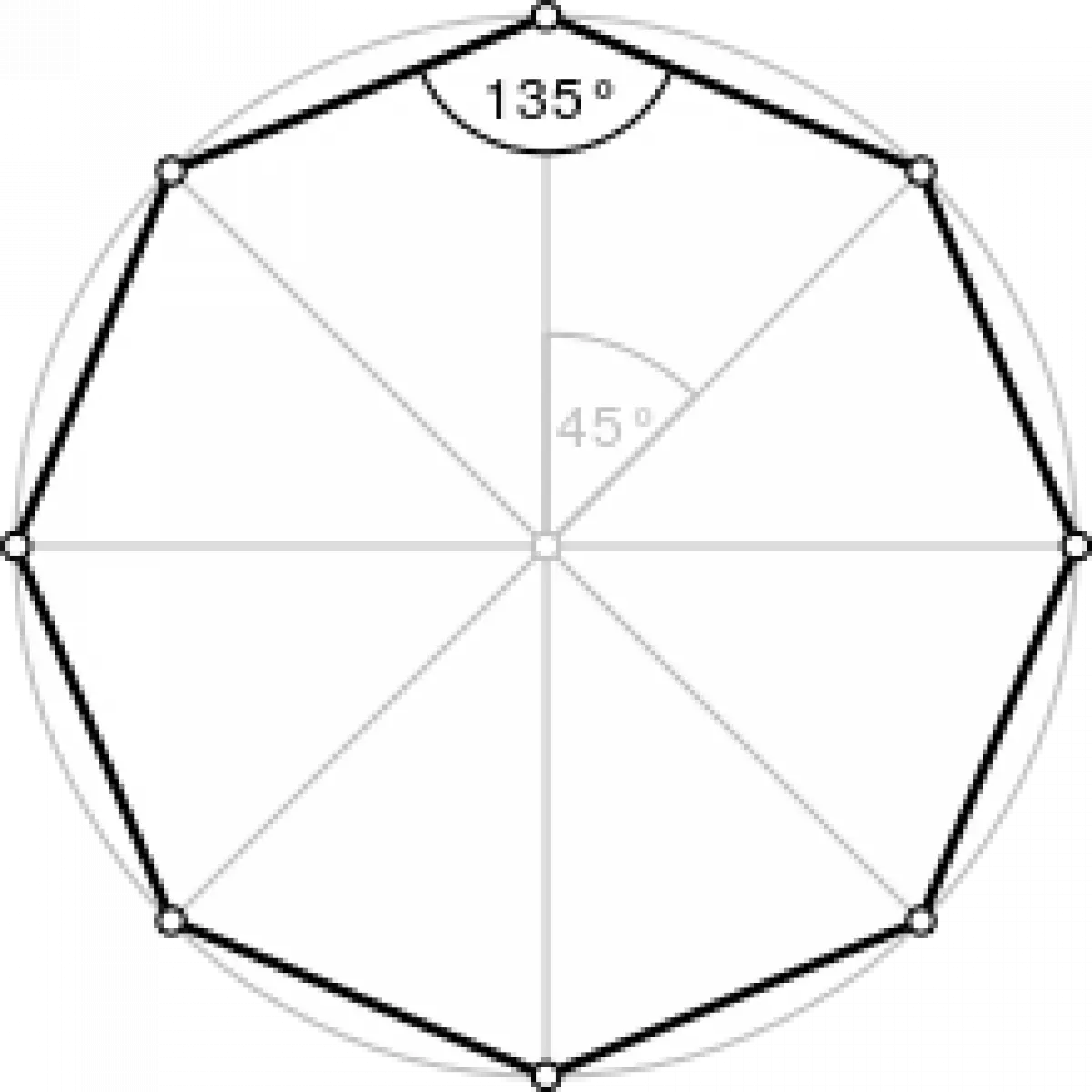
The sum of all internal angles of an octagon adds up to 1080°, and the sum of the external angles is 360° [^1^]. A regular octagon possesses eight lines of reflective symmetry and a rotational symmetry of order 8. Each vertex of a regular octagon has an internal angle of 135° and a central angle of 45° [^1^].

Area Computation
Determining the area of a regular octagon depends on its side length, span, or apothem. Using different formulas, you can find the area in terms of these measurements:
- In terms of side length, the area (A) can be calculated as A = 2 cot(π/8) * a^2, where a represents the side length [^1^].
- In terms of the circumradius (R), the area is A = 4 sin(π/4) R^2 = 2√2 R^2 [^1^].
- In terms of the apothem (r), the area is A = 8 tan(π/8) r^2 = 8(2-1) r^2 [^1^].

Construction
Constructing a regular octagon is a fascinating process. One method involves drawing a circle and two perpendicular diameters, and then bisecting the right angles formed to create the octagon's vertices [^1^]. Another method utilizes a straightedge and compass to achieve the desired shape [^1^].
Applications and Significance
The octagon's unique properties make it a highly valued shape in various fields. In architecture, octagonal floor plans are employed in structures such as the Dome of the Rock, the Tower of the Winds, and numerous churches worldwide [^1^]. Architects even utilize octagonal layouts for functional purposes in office buildings to separate different areas efficiently [^1^].
Beyond architecture, octagons can be found in bumper pool tables, and they have mathematical applications in number theory and tiling. They also appear in cultural symbols like the Rub el Hizb and the Octa Star [^1^].
Let the Octagon Enthrall You
As we unravel the wonders of the octagon, its allure becomes apparent. The symmetries, angles, and geometric intricacies make the octagon a captivating shape. Whether it's in architecture, design, or mathematics, the octagon continues to fascinate and inspire.
So, next time you encounter an octagon, take a moment to appreciate its beauty and the endless possibilities it represents.
References
[^1^]: Wikipedia contributors. (2024, January 25). Octagon. In Wikipedia, The Free Encyclopedia. Retrieved 10:51, November 19, 2024, from link.

















