In the vast and captivating realm of geometry, the polygon takes center stage. A polygon is a two-dimensional figure composed of line segments that connect to form a closed, polygonal chain. These line segments, known as edges or sides, meet at points called vertices or corners.

The number of sides on a polygon determines its name. For example, a triangle is a 3-sided polygon, while a pentagon has 5 sides.
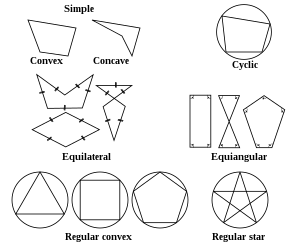
A polygon can be classified based on various attributes, such as convexity and intersection. Convex polygons have all interior angles measuring less than 180 degrees. Non-convex polygons, on the other hand, have angles that exceed 180 degrees. A simple polygon does not intersect itself, while a concave polygon has at least one interior angle greater than 180 degrees. Star-shaped polygons have their entire interior visible from at least one point, without crossing any edge. Self-intersecting polygons have line segments that cross over themselves.

Polygons can also possess symmetry and equality properties. Equiangular polygons have all corner angles equal, while equilateral polygons have all edges of the same length. Regular polygons exhibit both equilateral and equiangular properties. Cyclic polygons have all corners located on a single circle, known as the circumcircle, while tangential polygons have all sides tangent to an inscribed circle.

The study of polygons encompasses a rich history. The word "polygon" derives from the Greek words "polús" meaning "many" and "gōnía" meaning "corner" or "angle." The etymology suggests the abundance of angles in these geometric figures. The classification of polygons has been a topic of interest since ancient times, with artistic depictions of polygons dating back to the 7th century B.C.

The fascination with polygons extends beyond the field of geometry. These geometric figures can be observed in various natural formations, such as the hexagonal basalt columns at the Giant's Causeway in Northern Ireland and the honeycomb structure created by bees.

Expanding Our Understanding of Polygons
Polygons play a crucial role in computer graphics and modeling. They serve as fundamental building blocks for creating and rendering three-dimensional objects. Through advanced algorithms, polygons are transformed into three-dimensional shapes, allowing us to visualize intricate scenes on screens and other display systems.
Polygons also find their place in a variety of mathematical and scientific disciplines. They serve as essential tools for navigation, cartography, and measuring angles and areas. Moreover, polygons provide valuable insights and mathematical foundations for studying complex polytopes in higher dimensions.
The world of polygons extends far beyond the realms of geometry and mathematics. Their significance can be seen in the intricate patterns of crystals, the precise architecture of beehives, and even in philosophical discussions as examples of well-defined concepts that push the boundaries of human comprehension.

Exploring the intricacies of polygons unlocks a world of interconnectedness, where seemingly simple shapes reveal profound insights into the nature of our universe. Whether it's in the realms of art, science, or everyday life, polygons continue to captivate our imagination and expand our understanding of the world around us.
So next time you come across an intricate pattern or observe the symmetry of nature, take a moment to appreciate the beauty and significance of polygons in shaping our understanding of the world.









