Introduction
Have you ever wondered how to calculate the angles and properties of different polygons? Look no further! In this article, we will delve into the fascinating world of polygon formulas, unlocking the secrets behind these intriguing shapes. Whether you're a geometry enthusiast or simply curious about polygons, this article will provide you with all the information you need to understand and utilize polygon formulas effectively.
Types of Polygon
Before we dive into the formulas, let's first familiarize ourselves with the different types of polygons. Based on their angle measures and side lengths, polygons can be classified as follows:
- Regular Polygon - All the interior angles and sides have the same measure.
- Irregular Polygon - The interior angles and sides have different values.
- Convex Polygon - All the interior angles of a polygon are less than 180 degrees.
- Concave Polygon - Polygons that have one or more interior angles with a measure greater than 180 degrees.
The number of sides a polygon has determines its shape and name. Familiar examples include triangles, squares, pentagons, hexagons, and more.
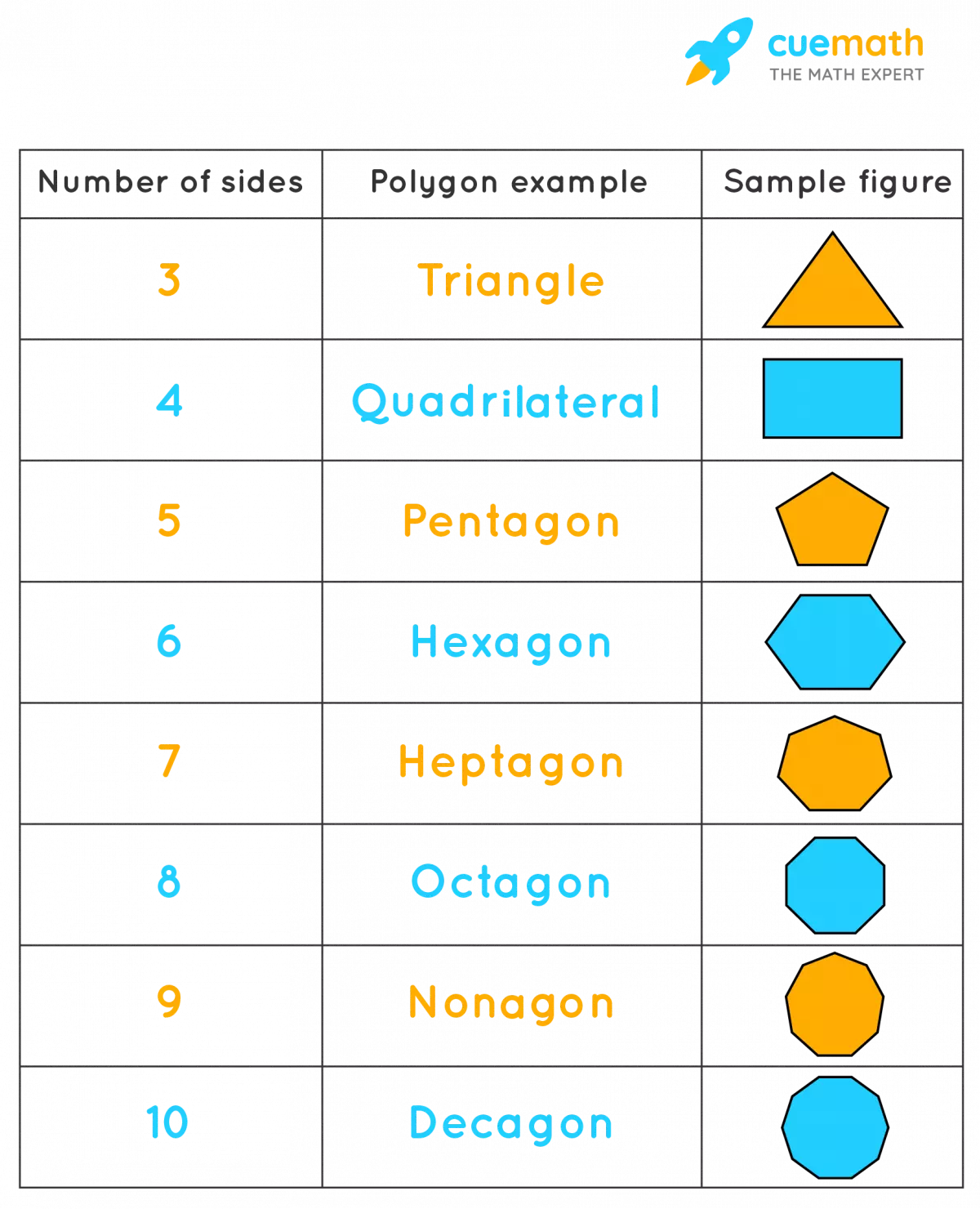Caption: Explore the variety of polygons.
What is a Polygon Formula?
Polygon formulas provide us with a comprehensive set of equations to uncover the mysteries of polygons. Let's break them down:
Formula 1: Sum of Interior Angles
For a regular polygon with 'n' sides, the sum of the interior angles is given by the formula: 180°(n-2).
Formula 2: Number of Diagonals
The number of diagonals in an "n-sided" polygon is calculated using the formula: [n(n-3)]/2.
Formula 3: Interior Angle Measure
The measure of each interior angle in a regular n-sided polygon is determined by the formula: (n-2)180°/n.
Formula 4: Exterior Angle Measure
The measure of each exterior angle in a regular n-sided polygon can be found using the formula: 360°/n.
Formula 5: Area
The area of a regular polygon can be calculated using the formula: (number of sides × length of one side × apothem)/2. The apothem's length is given as (l/2tan(180/n)), where 'l' represents the side length and 'n' denotes the number of sides.
Formula 6: Area in Terms of Perimeter
Alternatively, the area of a regular polygon can be calculated using the formula: Area = (Perimeter × apothem)/2. Here, the perimeter is equal to the number of sides multiplied by the length of one side.
Caption: Polygon formulas explained.
Properties of Polygons
Understanding the properties of polygons enhances our comprehension of these fascinating shapes. Some key properties include:
- The sum of interior angles of any quadrangle equals 360°.
- If at least one interior angle measures greater than 180 degrees, the polygon is called concave.
- A simple polygon does not intersect itself and has only one boundary. Conversely, a complex polygon intersects itself or has multiple boundaries.
Examples Using Polygon Formulas
Now, let's put our knowledge into practice with a few examples:
Example 1: Sum of Interior Angles of a Hexagon
Solution:
We know that a hexagon has six sides. Applying the polygon formula for the sum of interior angles, we have:
Interior angle sum = 180°(n-2) = 180°(6-2) = 180°(4) = 720°
Hence, the sum of the interior angles of a hexagon is 720°.
Example 2: Perimeter and Interior Angle of an Octagon
Solution:
Given that the polygon is an octagon with a side length of 7 cm, we can calculate its perimeter using the formula P = n × s:
P = 8 × 7 = 56 cm
To find the measure of each interior angle, we can use the polygon formula:
Interior Angle = [(n-2)180°]/n = [(8 - 2)180°] / 8 = (6 × 180°) / 8 = 135°
In summary, the perimeter of the octagon is 56 cm, and each interior angle measures 135 degrees.
Example 3: Sum of Interior Angles of a Triangle
Solution:
A triangle has three sides. By applying the polygon formula for the sum of interior angles, we obtain:
Interior angle sum = 180°(n-2) = 180°(3-2) = 180° (1) = 180°
Hence, the sum of the interior angles of a triangle is 180°.
Now that you've learned about polygon formulas, you can confidently explore the geometric world of polygons and unravel their hidden secrets. So go ahead and impress your friends with your newfound knowledge of polygons and their fascinating properties!
