An image of a regular hexagon
A regular hexagon is not just a shape with six equal sides; it holds fascinating properties that we will explore in this article. From its angles to its formulas for perimeter and area, we will delve into the intriguing world of this symmetrical polygon.
What Makes a Regular Hexagon Special?
A regular polygon is a two-dimensional convex shape with equal sides and interior angles. In the case of a regular hexagon, it boasts six equal sides and six identical interior angles.
The Interior Angles of a Regular Hexagon
The sum of interior angles in any polygon can be calculated using the formula S = (n-2) 180°, where n represents the number of sides. For a hexagon (n=6), the sum of interior angles is (6-2) 180° = 4 * 180° = 720°. Since all interior angles of a regular hexagon are equal, each angle measures 720°/6 = 120°.
This property leads to the interesting realization that a regular hexagon is composed of six equilateral triangles.
An image showing six equilateral triangles within a regular hexagon
The Proof: Six Equilateral Triangles
Although many "proofs" demonstrate that a regular hexagon is comprised of six equilateral triangles, they often involve complex steps. Let's follow a simpler proof to uncover this intuitive result.
We start by drawing the angle bisectors of two adjacent interior angles and labeling their intersection point as O. It becomes evident that triangle ΔOAB is an equilateral triangle since angle BAF = angle ABC = 120° (interior angles of a regular hexagon). The angle bisectors create two half angles of 60°, resulting in angle AOB also equaling 60°. Hence, ΔOAB is an equilateral triangle.
We proceed to connect point O with vertex C and compare triangles ΔOAB and ΔOCB.
An image depicting congruent equilateral triangles within a regular hexagon
By the side-angle-side postulate, triangles ΔOAB and ΔOCB are congruent. Therefore, ΔOCB is also an identical equilateral triangle to ΔOAB. We can repeat this process for the remaining sides, connecting point O with vertices D, E, and F. The outcome confirms that a regular hexagon consists of six identical equilateral triangles converging at its center, O.
Exploring Area and Perimeter
Since a regular hexagon is formed by six equilateral triangles, we can easily derive the formula for its area. It is six times the area of one of the equilateral triangles.
An equilateral triangle's area can be calculated using the formula AreaΔequilateral = (s^2 * √3)/4, where s represents the length of its side.
Hence, the area of the hexagon can be expressed as: Area⬡hex = 6 (s^2 √3)/4 = 3√3 * s^2/2
When it comes to perimeter, all sides of a regular hexagon are equal. Therefore, the perimeter of a regular hexagon (P⬡hex) is simply the sum of its six sides: 6s.
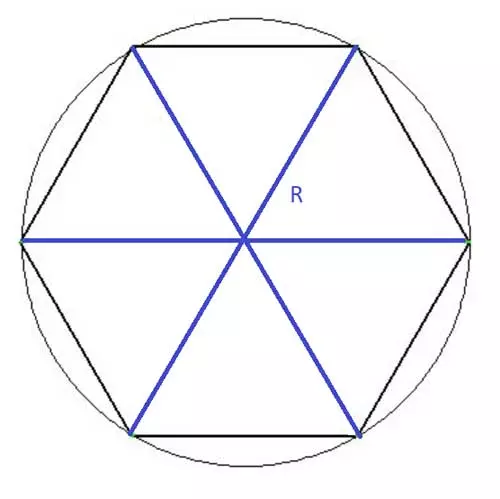
Meet the Radius
The radius of a regular polygon is the distance between its center and any of its vertices. In the case of a regular hexagon, this distance remains the same for all vertices.
We have already established that the center of a regular hexagon forms an equilateral triangle with its edges. Consequently, the radius (R) of the hexagon is equal to the length of each side. This also allows us to inscribe a regular hexagon within a circle with a radius of R.
An illustration of a regular hexagon inscribed in a circle
Conclusion
A regular hexagon is not just an ordinary six-sided polygon; it is a captivating geometric figure with symmetrical characteristics. Its interior angles, area, perimeter, and even the radius encompass intriguing properties that showcase the beauty of mathematics. Exploring the secrets of shapes like the regular hexagon opens a gateway to a world of geometric wonder.
