Regular Polygon: Understanding the Definition, Properties, and Examples

Introduction

Have you ever wondered what a regular polygon is and what makes it unique? In this article, we will delve into the world of polygons, exploring their definition, properties, and examples. By the end, you'll have a clear understanding of this fascinating geometric concept and its applications.

What Is a Polygon?

A polygon is a two-dimensional enclosed figure formed by connecting three or more straight lines. These "flat figures" come in various shapes and sizes. For example, a square is a polygon with four equal-length sides. Take a look at the image below for more examples:

Examples of polygons

Parts of a Polygon

A polygon consists of three main parts:

Sides

Sides are line segments that connect two vertices, forming the boundaries of the polygon.

Vertices

Vertices are the points where two sides meet. They define the corners of the polygon.

Angles

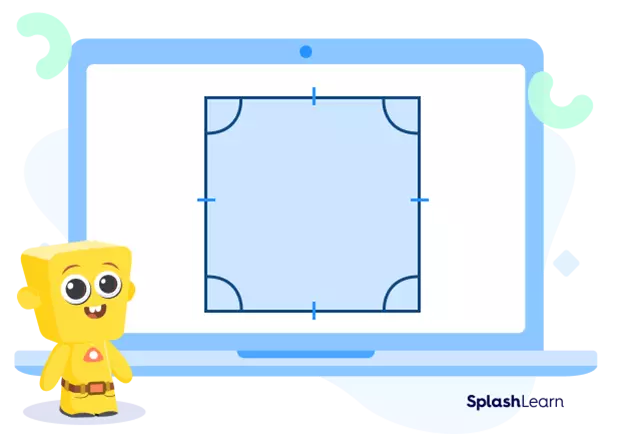
Polygons have both interior and exterior angles. The interior angle is formed within the enclosed surface of the polygon, while the exterior angle is the angle formed outside the polygon. Take a look at the image below for a visual representation:

Parts of a polygon

What Are Regular Polygons?

When all the sides and interior angles of a polygon are equal, we refer to it as a regular polygon. Examples of regular polygons include squares and equilateral triangles. Not only do regular polygons have congruent sides, but their angles are also equal, making them equiangular.

Regular polygon

Properties of Regular Polygons

The properties of regular polygons are as follows:

• All sides of a regular polygon are equal in length.
• All interior angles of a regular polygon are equal in measure.
• The sum of the exterior angles of a regular polygon is always 360°.

Perimeter of a Regular Polygon

The perimeter of a regular polygon is the sum of all its sides. In a regular polygon with n sides, the perimeter is equal to n times the length of a side. For example, if the side of a regular polygon measures 6 cm and the polygon has 5 sides, the perimeter would be 30 cm.

Sum of Interior Angles of a Regular Polygon

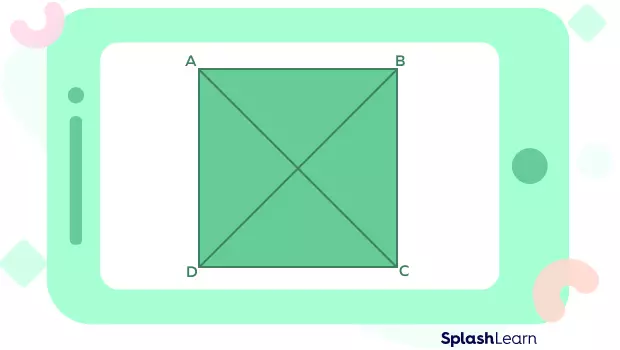
For a regular polygon with n sides, the sum of its interior angles can be calculated using the formula (n - 2) × 180°. Let's take a regular polygon with 6 sides as an example. The sum of its interior angles would be (6 - 2) × 180° = 720°.

Measure of Each Interior Angle of a Regular Polygon

Since regular polygons are equiangular, the measure of each interior angle can be calculated by dividing the sum of interior angles by the number of sides. For instance, in an 8-sided regular polygon, each interior angle would be (8 - 2) × 180° / 8 = 135°.

Measure of Each Exterior Angle of a Regular Polygon

The measure of each exterior angle of a regular polygon is determined by dividing 360° (the sum of all exterior angles) by the number of sides. Therefore, for an n-sided regular polygon, each exterior angle measures 360° / n.

Number of Diagonals of a Regular Polygon

The number of diagonals in a polygon with n sides can be calculated using the formula n(n - 3) / 2. This accounts for the fact that each vertex connects to (n - 3) vertices, and to avoid double counting, we divide by two. For example, a regular polygon with 4 sides (a square) has 2 diagonals.

Number of Triangles of a Regular Polygon

The number of triangles formed by joining the diagonals from one corner of a regular polygon is equal to n - 2, where n represents the number of sides. For a polygon with 4 sides, there would be 2 triangles formed.

Lines of Symmetry of a Regular Polygon

A line of symmetry divides a shape or object into identical halves. In regular polygons, the number of lines of symmetry is equal to the number of sides (n). For example, a square has 4 sides, so it also possesses 4 lines of symmetry.

Order of Symmetry of a Regular Polygon

The order of rotational symmetry in a regular polygon is equal to the number of sides (n). This means that when a regular polygon is rotated a certain number of times (the order), it will align perfectly with its original position. The angle of rotational symmetry in a regular polygon can be calculated using the formula 360° / n. For example, a square has 4 sides, resulting in an order of rotational symmetry of 4 and an angle of 90°.

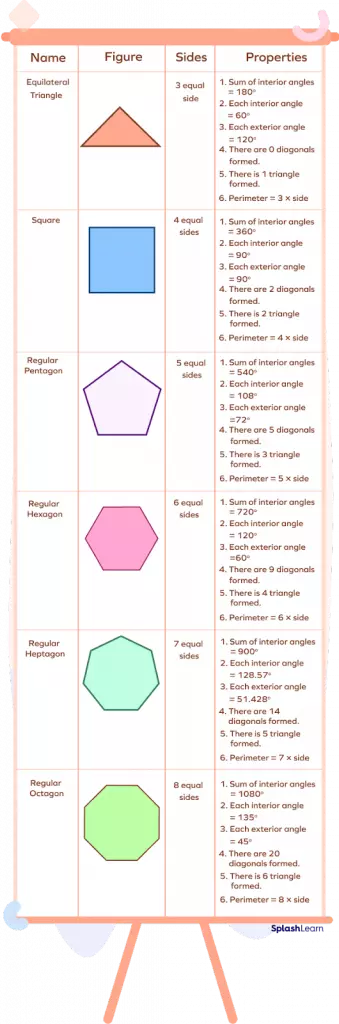
Different Regular Polygons

Here are some examples of regular polygons:

Fun Fact!

Regular polygons have played a significant role in art, architecture, and even nature. From the beautiful symmetry of snowflakes to the stunning patterns in Islamic geometric art, regular polygons continue to captivate and inspire us.

Solved Examples on Regular Polygon

Let's solve a couple of examples to solidify our understanding:

Example 1: Find the number of diagonals of a regular polygon with 12 sides.

Solution: The number of diagonals of an n-sided polygon can be calculated using the formula n(n - 3) / 2. For our case, the number of diagonals would be: 12 × (12 - 3) / 2 = 54 diagonals.

Example 2: If each interior angle of a regular polygon measures 120°, how many sides does it have?

Solution: We can use the formula (n - 2) × 180° / n to find the number of sides. Let's substitute the given angle: 120° = (n - 2) × 180° / n.

Simplifying the equation, we get: 120n = 180n - 360, 60n = 360, n = 6.

Therefore, the number of sides in the regular polygon is 6.

Example 3: Can a regular polygon have an internal angle of 100° each?

Solution: To determine if this is possible, we need to calculate the exterior angle of the polygon. The exterior angle is given by 180° - internal angle. So, the exterior angle in this case would be 180° - 100° = 80°.

Using the formula 360° / n for the exterior angle, we find: 80° = 360° / n, n = 360° / 80°, n = 4.5.

Since the number of sides cannot be in decimal form, a regular polygon with internal angles of 100° each is not possible.

Practice Problems on Regular Polygon

Now that we have covered the fundamentals, why not put your knowledge to the test? Try solving these practice problems to enhance your understanding of regular polygons:

1. Find the measure of each interior angle of a regular polygon with 10 sides.
2. Determine the number of diagonals in a regular polygon with 7 sides.

Frequently Asked Questions on Regular Polygon

1. Question: What is a polygon? Answer: A polygon is a two-dimensional enclosed figure formed by connecting three or more straight lines.

2. Question: What are regular polygons? Answer: Regular polygons are polygons where all sides and interior angles are equal.

3. Question: How do you calculate the perimeter of a regular polygon? Answer: The perimeter of a regular polygon is the sum of all its sides.

4. Question: What is the order of symmetry of a regular polygon? Answer: The order of symmetry of a regular polygon is equal to the number of its sides.

Now that you have a solid grasp of regular polygons, you can appreciate their beauty and elegance in various aspects of life. From intricate architecture to intricate mathematical concepts, regular polygons continue to fascinate us with their symmetry and mathematical properties. So, the next time you come across a geometric shape, take a moment to observe its regularity and appreciate the wonders of mathematics in our world.