Trong một đa giác, tổng góc phụ thuộc vào số cạnh và số đỉnh của nó. Có hai loại góc trong một đa giác - Góc nội và Góc ngoại. Hãy tìm hiểu về các phương pháp khác nhau để tính tổng góc nội và tổng góc ngoại của một đa giác.
Loại đa giác
Có 2 loại góc trong một đa giác đều - Góc nội và Góc ngoại. Góc nội là các góc nằm bên trong một hình dạng, thông thường là một đa giác. Góc ngoại của một đa giác là góc giữa một cạnh và cạnh tiếp theo.
Ví dụ, ở tam giác sau, chúng ta có các góc nội A, B và C. Các góc nội trong một đa giác đều bằng nhau. Do đó, để tìm tổng góc nội của một đa giác, chúng ta sử dụng công thức: Tổng góc nội = (n − 2) × 180°, trong đó 'n' là số cạnh của một đa giác.
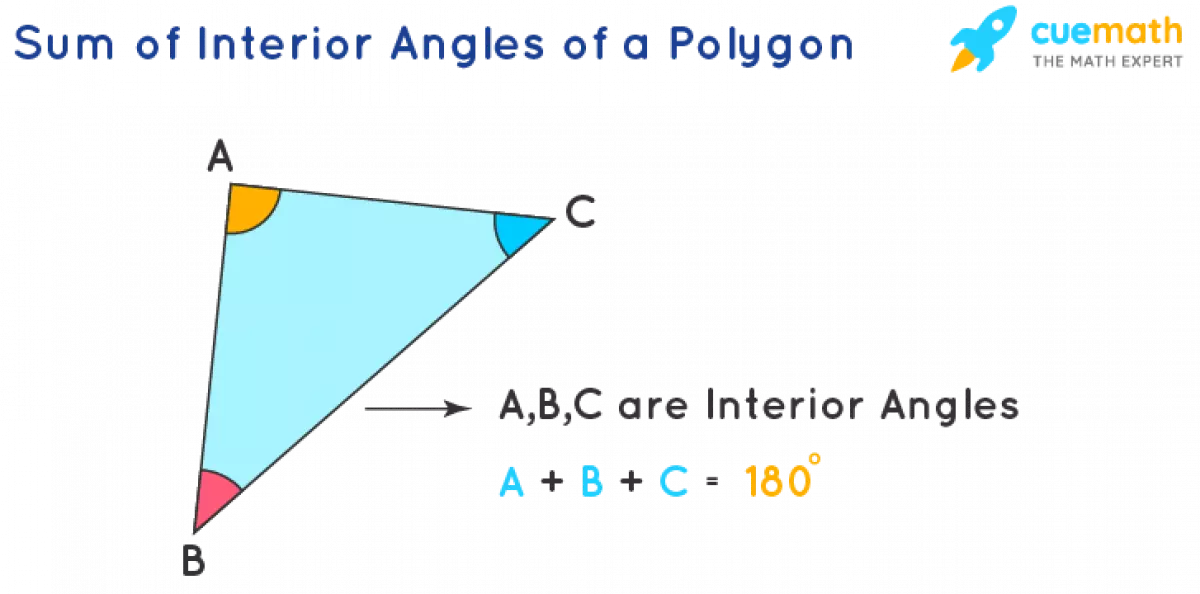Tam giác: ví dụ về góc nội trong một đa giác.
Cách khác để tính tổng góc nội là kiểm tra số tam giác được tạo thành bên trong đa giác bằng các đường chéo. Vì tổng góc nội của một tam giác là 180°, tổng góc nội của bất kỳ đa giác nào cũng có thể được tính bằng cách nhân 180° với số tam giác được tạo thành bên trong đa giác. Ví dụ, một tứ giác có thể được chia thành hai tam giác bằng cách sử dụng các đường chéo, do đó, tổng góc nội của một tứ giác là 2 × 180° = 360°. Tương tự, một ngũ giác có thể được chia thành 3 tam giác, vì vậy tổng góc nội của ngũ giác sẽ là 3 × 180° = 540°.
Ví dụ: Hãy tính tổng góc nội của một lục giác.
Giải: Lục giác có 6 cạnh, do đó, n = 6. Tổng góc nội của một đa giác đều, S = (n − 2) × 180 S = (6-2) × 180° ⇒ S = 4 × 180 ⇒ S=720°. Vì vậy, tổng góc nội của một lục giác là 720°.
Góc ngoại của một đa giác (góc bên ngoài) là góc được tạo bởi một cạnh và phần tiếp theo của cạnh kề của đa giác đó. Hãy xem các góc ngoại được hiển thị trong đa giác dưới đây.
Đa giác: ví dụ về góc ngoại trong một đa giác.
Tổng góc ngoại của một đa giác có giá trị bằng 360°. Điều này có thể được chứng minh bằng các bước sau:
- Chúng ta biết rằng tổng góc nội của một đa giác đều với 'n' cạnh = 180 (n-2).
- Góc nội và góc ngoại tại mỗi đỉnh tạo thành một cặp tuyến tính. Do đó, có 'n' cặp tuyến tính trong đa giác. Bây giờ, vì mỗi cặp tuyến tính có tổng 180°, tổng của tất cả các cặp tuyến tính sẽ là: 180n°.
- Vậy, tổng góc ngoại = Tổng của tất cả các cặp tuyến tính - Tổng góc nội.
- Điều này có nghĩa là: Tổng góc ngoại = 180n - 180(n-2) = 180n - 180n + 360. Do đó, tổng góc ngoại của một đa giác có 5 cạnh bằng 360°.
Bài viết liên quan:
Xem các bài viết thú vị liên quan đến Tổng góc trong một đa giác. Bấm để biết thêm chi tiết!
- Công thức tổng góc
- Công thức góc nội
- Đa giác
