Geometry can be intriguing, with its fascinating theorems and properties that govern the shapes and figures we encounter in everyday life. One such theorem is the Angle Sum Property of a Triangle, also known as the Triangle Sum Theorem. In this article, we will dive into the definition of this theorem, explore its applications, and provide examples to enhance your understanding.
What is the Angle Sum Property of a Triangle?
The Angle Sum Property of a Triangle states that the sum of the three interior angles of any triangle is always 180 degrees. This fundamental theorem holds true for all types of triangles, be it right triangles, obtuse triangles, or acute triangles. No matter the shape or size of the triangle, the sum of its internal angles will always amount to 180 degrees.

The Angle Sum Property of a Triangle Theorem
The Angle Sum Property of a Triangle Theorem is a concise statement that affirms the Angle Sum Property of a Triangle. It reiterates that the sum of all three internal angles of a triangle is equal to 180 degrees. This theorem is also referred to as the Triangle Sum Theorem.

According to the Angle Sum Property of a Triangle Theorem, in a triangle labeled ABC, the sum of angles A, B, and C is equal to 180 degrees:
∠A + ∠B + ∠C = 180°Let's take a look at an example to illustrate this theorem further.
Example: In triangle PQR, if angle P measures 60 degrees and angle Q measures 70 degrees, what is the measure of angle R?
According to the Angle Sum Property of a Triangle Theorem, in triangle PQR:
∠P + ∠Q + ∠R = 180°Substituting the given values:
60° + 70° + ∠R = 180°
130° + ∠R = 180°
∠R = 50°Therefore, the measure of angle R is 50 degrees.
Triangle Sum Theorem Proof
To solidify our understanding of the Angle Sum Property of a Triangle Theorem, let's explore a proof that verifies its validity.

In the figure above, triangle ABC is depicted, with sides AB, BC, and CA, and vertices A, B, and C. The goal is to prove that the sum of angles A, B, and C is equal to 180 degrees.
To prove: ∠A + ∠B + ∠C = 180°
Construction: Draw a line DE passing through vertex B, parallel to side AC.
At point B, two angles are formed: ∠1 and ∠2.
Since AB is a transversal for the parallel lines DE and AC, we can conclude that:
∠1 = ∠A (since the pair of alternate interior angles are equal) ∠2 = ∠C
Now, since ∠1, ∠B, and ∠2 lie on a straight line, their sum is equal to 180 degrees:
∠1 + ∠B + ∠2 = 180° ... (I)
Substituting the values for ∠1 and ∠2:
∠A + ∠B + ∠C = 180°
Hence, the sum of angles A, B, and C is 180 degrees, proving the Triangle Sum Theorem.
The Exterior Angle Theorem
In addition to the Angle Sum Property of a Triangle, another intriguing theorem related to triangles is the Exterior Angle Theorem. This theorem states that "an exterior angle of a triangle is equal to the sum of its two opposite interior angles."

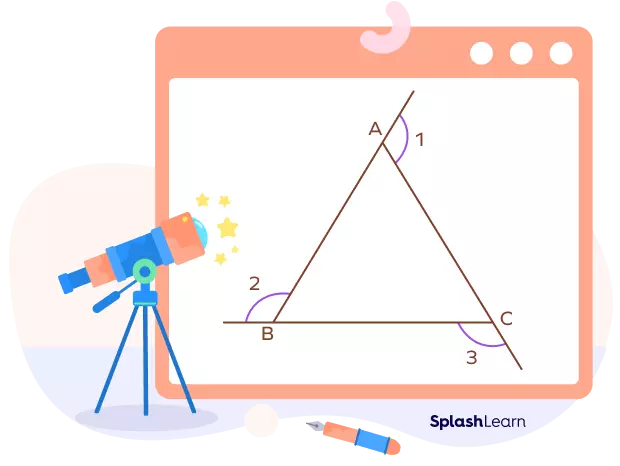
In the given triangle ABC, angles A, B, and C are the interior angles, while angles 1, 2, and 3 are the exterior angles. According to the Exterior Angle Theorem:
∠A + ∠B + ∠C = 180° (angle sum property) ... (I)
∠A + ∠1 = 180° (linear pair angle) ... (II)From equations (I) and (II), we can derive the equations for the other two exterior angles, ∠2 and ∠3:
∠2 = ∠A + ∠C
∠3 = ∠A + ∠BIn summary:
Facts about Angle Sum Property of a Triangle
Here are some interesting facts related to the Angle Sum Property of a Triangle:
- The theorem of the angle sum property of triangles holds true for all types of triangles.
- The sum of all exterior angles of a triangle is equal to 360 degrees.
- The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.
- A rectangle can be divided into two right triangles by drawing a line from one corner to the opposite corner.
- The study of the relationship between the sides and angles of triangles is known as trigonometry.
- Due to their high strength, triangle shapes are frequently utilized in construction.
- In North Carolina, there are three cities—Raleigh, Durham, and Chapel Hill—that are often referred to as "the Triangle."
- The sum of all exterior angles of a triangle is equal to 360 degrees.
Conclusion
In this article, we have explored the Angle Sum Property of a Triangle and its significance in geometry. We have examined the Angle Sum Property of a Triangle Theorem, presented a proof that supports this theorem, and discussed the Exterior Angle Theorem. Additionally, we have shared some interesting facts about triangles to deepen your understanding. Next time you encounter a triangle, remember the Angle Sum Property, and enjoy exploring its numerous applications!
Solved Examples on Angle Sum Property of a Triangle
Here are some examples that demonstrate the application of the Angle Sum Property of a Triangle:
- In a triangle ABC, if ∠A = 60° and ∠B = 40°, what is the measure of angle C?
Solution:
In ΔABC, we are given that ∠A = 60° and ∠B = 40°.
We know that the sum of angles in a triangle is 180°.
∠A + ∠B + ∠C = 180°
60° + 40° + ∠C = 180°
∠C = 180° - (60° + 40°)
∠C = 180° - 100°
∠C = 80°Therefore, the measure of angle C is 80°.
- One of the acute angles in a right-angled triangle is 40°. Using the angle sum theorem, determine the measure of the other angle.
Solution:
Let ΔABC be a right-angled triangle with right angle at B.
∠B = 90°
∠A = 40°, and we need to find ∠C.
We know that the sum of angles in a triangle is 180°.
∠A + ∠B + ∠C = 180°
40° + 90° + ∠C = 180°
∠C = 180° - (40° + 90°)
∠C = 180° - 130°
∠C = 50°Therefore, ∠A = ∠C = 50°.
- The measures of interior angles of a triangle are (2x - 20)°, (3x - 10)°, and 2x°. Find the values of all three angles of the triangle.
Solution:
We know that the sum of angles in a triangle is 180°.
(2x - 20)° + (3x - 10)° + 2x° = 180°
7x - 30 = 180
7x = 180 + 30
7x = 210
x = 210 / 7
x = 30Therefore, the angles are 40°, 80°, and 60°.
- Is it possible to construct a triangle with internal angles 43°, 49°, and 91°?
Solution:
Given the measurements of angles 43°, 49°, and 91°.
Here, 43° + 49° + 91° = 183°, which is not equal to 180°.
We know that the sum of angles in a triangle is 180°.
Therefore, it is not possible to construct a triangle with angles measuring 43°, 49°, and 91°.
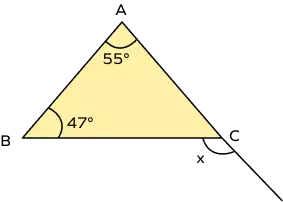
- In the figure given below, determine the value of "x".

Solution:
In the above figure, ∠x is an exterior angle, and ∠A = 55° and ∠B = 47° are given as interior angles.
According to the exterior angle property, an exterior angle of a triangle is equal to the sum of its two interior opposite angles.
So, ∠x = ∠A + ∠B = 55° + 47° = 102°
Hence, x = 102°.
Practice Problems on Angle Sum Property of a Triangle
To further enhance your understanding of the Angle Sum Property of a Triangle, here are some practice problems for you to solve:
-
In a triangle XYZ, the measure of angle X is 70°, and the measure of angle Y is 40°. Find the measure of angle Z.
-
The measures of the interior angles of a triangle are (4x - 10)°, (6x - 20)°, and (8x + 30)°. Find the values of all three angles of the triangle.
-
Determine the measure of angle x in the following triangle:

-
Given a triangle ABC, if the measure of angle A is twice the measure of angle B and three times the measure of angle C, find the measures of angles A, B, and C.
-
Can a triangle have interior angles measuring 80°, 50°, and 60°? Explain your answer.
Take your time to solve these problems and verify your answers. Remember to apply the Angle Sum Property of a Triangle to find the missing angles accurately!
Frequently Asked Questions on Angle Sum Property of a Triangle
Q: Is the Angle Sum Property of a Triangle theorem applicable to all types of triangles?
A: Yes, the Angle Sum Property of a Triangle theorem holds true for all types of triangles, including right triangles, obtuse triangles, and acute triangles.
Q: What is the sum of the exterior angles of a triangle?
A: The sum of the exterior angles of a triangle is always 360 degrees.
Q: Are there any practical applications of the Angle Sum Property of a Triangle?
A: Yes, the Angle Sum Property of a Triangle is widely used in various fields, such as architecture, engineering, and physics. It helps in calculations involving triangles and aids in determining unknown angles and sides of triangles.
Q: How is the Angle Sum Property of a Triangle related to trigonometry?
A: Trigonometry is the study of relationships between the sides and angles of triangles. The Angle Sum Property of a Triangle forms the basis for many trigonometric calculations and proofs.
Q: Why are triangles frequently utilized in construction?
A: Triangles are frequently used in construction due to their inherent stability and strength. The triangular shape distributes forces evenly and provides structural stability, making it a preferred choice in various architectural designs.
Remember these key insights about the Angle Sum Property of a Triangle, and you'll find yourself unraveling the mysteries of triangles with ease. Happy learning and exploring the fascinating world of geometry!

















