Have you ever marveled at the elegance of geometric shapes? Among them, the regular decagon stands out with its ten sides and ten vertices. In this article, we will dive into the theoretical background of regular decagons, explore their unique properties, and even learn how to draw one using simple tools. Let's embark on this journey and discover the captivating world of regular decagons!
Definitions
A decagon can be either convex or concave, depending on the arrangement of its sides and angles. A convex decagon has all its interior angles less than 180°, while a concave decagon has at least one angle greater than 180°. A decagon is classified as regular when its sides and interior angles are equal. On the other hand, a decagon with equal sides but unequal interior angles is known as an equilateral decagon. Any decagon that doesn't fit these criteria is considered irregular.
 Image: A visual representation of regular and equilateral decagons
Image: A visual representation of regular and equilateral decagons
The sum of the internal angles of any decagon, whether convex or concave, is always 1440°. This can be easily understood by visualizing how many triangles can be formed within the decagon. By drawing straight lines between all the vertices, we can see that eight triangles can be created. Since the sum of internal angles in one triangle is 180°, the total angles in the eight triangles add up to 1440°.
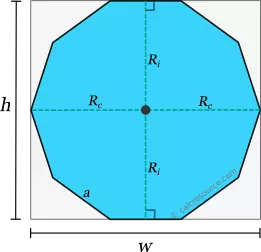 Image: The diagonals of a decagon separate its interior into eight triangles
Image: The diagonals of a decagon separate its interior into eight triangles
Properties of Regular Decagons
Symmetry
Regular decagons possess ten axes of symmetry. Five of these axes pass through diagonally opposite vertices, while the remaining five pass through the midpoints of opposite edges. All the axes converge at a common point, which is the center of the decagon.
 Image: Axes of symmetry of a regular decagon
Image: Axes of symmetry of a regular decagon
Interior Angle and Central Angle
Since regular decagons have equal interior angles, each angle measures 144°. The central angle, which is the angle between two successive diagonals of the decagon, also measures 36°. In the internal triangle formed by two diagonals and an edge of the decagon, the angles adjacent to the edge are equal to 72°, which is half of the interior angle.
The sum of the interior and central angles of a regular decagon is 180°:
144° + 36° = 180°
Circumcircle and Incircle
A circumcircle, or circumscribed circle, can be drawn around a regular decagon, passing through all ten vertices. The center of this circle coincides with the center of the decagon, and the diagonals of the decagon serve as its diameters. The radius of the circumcircle, known as the circumradius, can be calculated in relation to the edge length.
Similarly, an inscribed circle, or incircle, can be drawn within the regular decagon, touching all ten edges. The radius of the incircle, known as the inradius, also relates to the edge length.
 Image: Circumscribed and inscribed circles of a regular decagon
Image: Circumscribed and inscribed circles of a regular decagon
Area and Perimeter
The area of a regular decagon can be divided into ten identical isosceles triangles. The height of each triangle is equal to the inradius, and thus, the area of each triangle is 1/2 times the product of the base (edge length) and the inradius. The total area of the decagon can be calculated by multiplying the area of one triangle by ten.
The perimeter of a regular decagon is simply the sum of the lengths of its ten edges.
Bounding Box
The bounding box of a regular decagon is the smallest rectangle that encloses the shape completely. The height of the bounding box is twice the inradius, while the width is twice the circumradius. These dimensions can be approximated using the edge length.
How to Draw a Regular Decagon
With just a ruler and compass, you can construct a regular decagon based on its circumradius. Follow these steps:
- Draw a line slightly larger than the desired diameter of the circumcircle.
- Mark two points on the line: one for the center of the decagon (point O) and another on the circumcircle (point A). The distance between O and A represents the circumradius. Draw a circle with point O as the center, passing through A.
- Construct two circular arcs with centers at points A and B, both with a radius slightly larger than the circumradius. Mark the two points where the arcs intersect.
- Draw a line passing through the intersections of the arcs and point O. Mark two more points (1 and 6) where this line intersects the circumcircle.
- Place the compass tip on point A and construct a new arc passing through point O. Mark the two points where the arc intersects the circumcircle.
- Draw a line passing through the two intersection points from the previous step and point O. Mark the intersection point M between this line and the linear segment OA.
- Draw a line from point 1 to point M.
- With the compass tip on point M, draw a circular arc passing through point O. Mark point N, where this arc intersects with the line drawn in the previous step.
- Using point 1 as the center, draw a circular arc passing through point N. Mark the two points (2 and 10) where the arc intersects the circumcircle.
- Repeat the previous step, using each newly marked point as the center of the next arc. Continue this process until all ten vertices of the decagon are marked.
- Connect the marked points with straight lines, and voila! The regular decagon is complete.
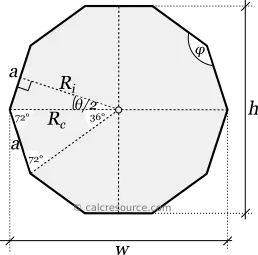 Image: Step-by-step procedure for drawing a regular decagon
Image: Step-by-step procedure for drawing a regular decagon
Examples
Regular decagons can be found in various contexts, such as architecture, art, and design. Their symmetrical and harmonious nature makes them visually appealing. Explore the possibilities of regular decagons and unleash your creative side!
Regular Decagon Cheat-Sheet
Refer to the following table for a concise list of formulas related to regular decagons:
| Quantity | Formula | Approximation |
|---|---|---|
| Circumradius | R_c = 1.618a | |
| Inradius | R_i = 1.539a | |
| Height | h = 3.078a | |
| Width | w = 3.236a | |
| Area | A = 7.694a^2 |
Regular decagons are fascinating geometric shapes with unique properties. Their symmetry, angles, and circles have captivated mathematicians and designers alike. Next time you encounter a regular decagon, take a moment to appreciate its elegance and precision.

















