Have you ever wondered about the mysterious angles that form when a transversal crosses two parallel lines? These angles, known as consecutive interior angles, hold a fascinating secret. In this article, we will explore the properties and theorems associated with consecutive interior angles, shedding light on their importance in the world of geometry.
Unveiling the Definition of Consecutive Interior Angles
Consecutive interior angles are pairs of non-adjacent interior angles that lie on the same side of a transversal. To put it simply, they are angles that appear next to each other on the inner side of the transversal. Let's take a closer look at the defining characteristics of consecutive interior angles:
- Consecutive interior angles have different vertices.
- They are situated between two lines.
- They exist on the same side of the transversal.
- They share a common side.
To better visualize this concept, take a look at the image below:
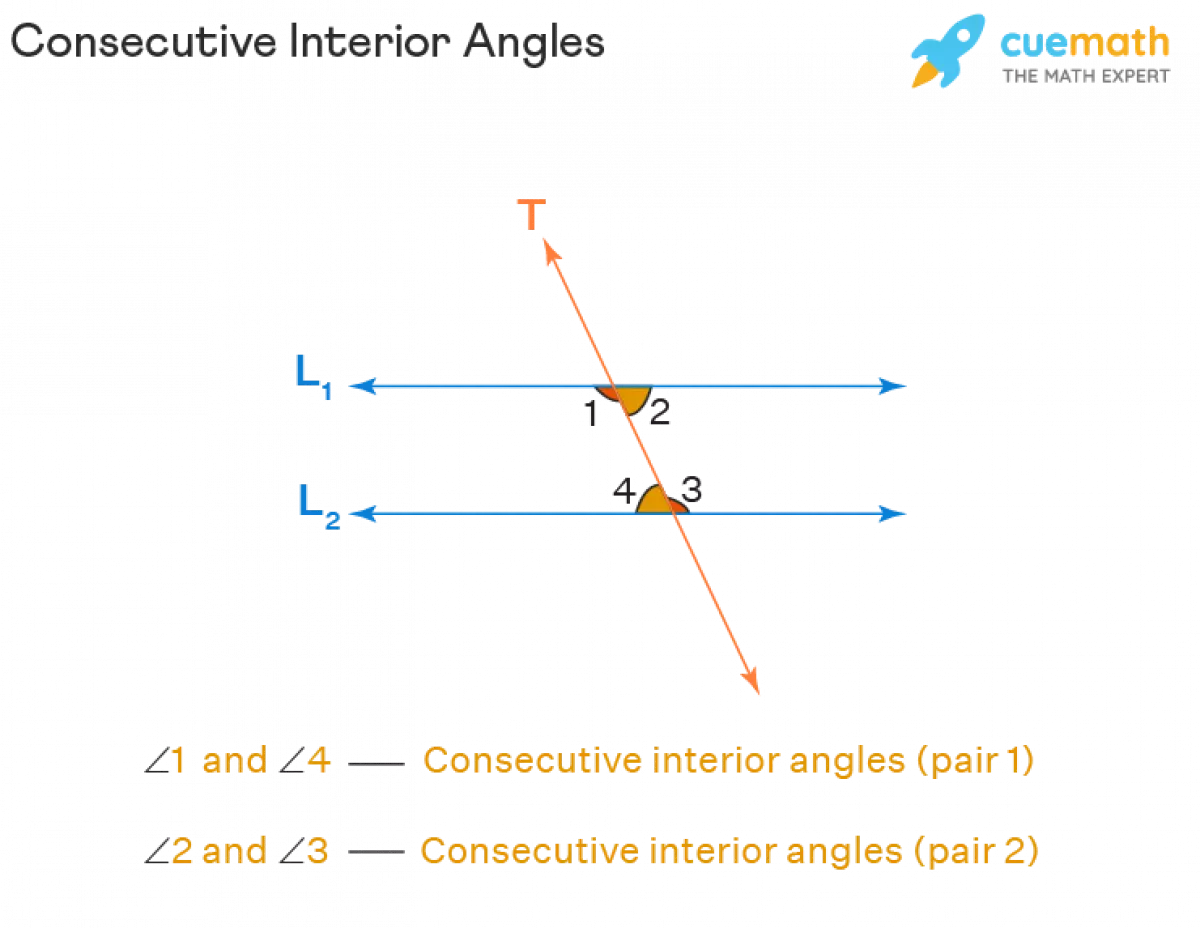Image: Consecutive Interior Angles
In the given image, the parallel lines L1 and L2 are intersected by the transversal T. The consecutive interior angles in this scenario are:
- ∠1 and ∠4
- ∠2 and ∠3
A Universe of Angles Formed by a Transversal
When a transversal crosses a pair of parallel lines, it creates more than just consecutive interior angles. Other types of angles also emerge, such as corresponding angles, alternate interior angles, and alternate exterior angles. Explore the image below to familiarize yourself with these various angles and their properties:
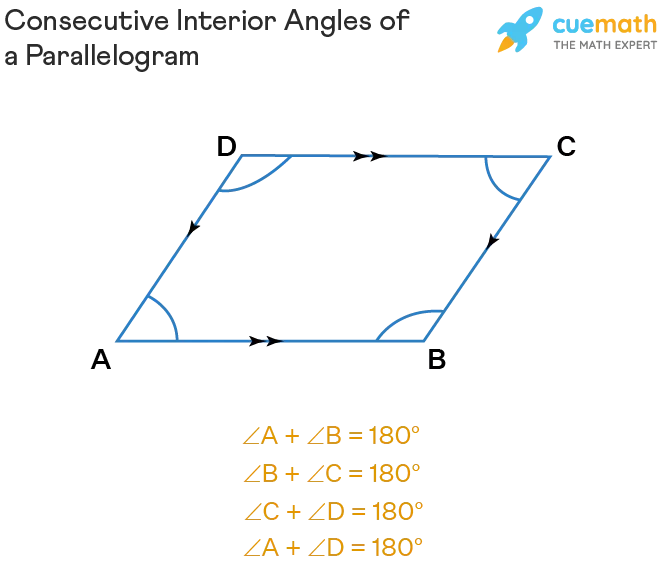Image: Angles Formed By a Transversal
To help you understand these angles further, here are their distinctive properties:
Corresponding Angles
Corresponding angles are angles that:
- Have different vertices.
- Exist on the same side of the transversal and are located above or below the lines.
- Are always equal.
Whenever a transversal intersects two parallel lines, the corresponding angles formed are always equal.
Alternate Interior Angles
Alternate interior angles are angles that:
- Have different vertices.
- Exist on opposite sides of the transversal.
- Reside between the interior of the two lines.
Similar to corresponding angles, when a transversal intersects two parallel lines, the alternate interior angles formed are always equal.
Alternate Exterior Angles
Alternate exterior angles are angles that:
- Have different vertices.
- Exist on opposite sides of the transversal.
- Are exterior to the lines.
Likewise, when a transversal intersects two parallel lines, the alternate exterior angles formed are always equal.
Consecutive Interior Angles
Lastly, we come back to the star of our article - consecutive interior angles. These angles have the following characteristics:
- Have different vertices.
- Lie between two lines.
- Exist on the same side of the transversal.
When a transversal intersects two parallel lines, the consecutive interior angles are always supplementary. This means that the sum of the consecutive interior angles equals 180°.
The Consecutive Interior Angle Theorem Unveiled
The relationship between consecutive interior angles is determined by the consecutive interior angle theorem. This theorem states that if a transversal intersects two parallel lines, each pair of consecutive interior angles is supplementary.
To illustrate this theorem, let's examine the figure below:
Image: Consecutive Interior Angles Theorem
Given that lines L1 and L2 are parallel, and T is the transversal, we can deduce the following:
- ∠1 = ∠5 (corresponding angles with parallel lines) - (Equation 1)
- ∠1 + ∠4 = 180° (Linear pair angles are supplementary) - (Equation 2)
By substituting ∠1 as ∠5 in Equation (2), we obtain: ∠5 + ∠4 = 180°. Similarly, we can show that ∠3 + ∠6 = 180°. Additionally:
- ∠2 = ∠6 (corresponding angles with parallel lines) - (Equation 3)
- ∠2 + ∠3 = 180° (Linear pair angles are supplementary) - (Equation 4)
By substituting ∠2 as ∠6 in Equation (4), we get: ∠6 + ∠3 = 180°.
From this analysis, we can conclude that ∠4 + ∠5 = 180° and ∠3 + ∠6 = 180°.
Therefore, we have proven that consecutive interior angles are indeed supplementary.
The Converse of Consecutive Interior Angle Theorem
The converse of the consecutive interior angle theorem states that if a transversal intersects two lines in such a way that a pair of consecutive interior angles is supplementary, then the two lines are parallel. Let's examine the proof of this theorem and its converse:
Referring to the same figure, we are given the following:
- ∠5 + ∠4 = 180° (Consecutive Interior angles) - (Equation 1)
Since ∠1 and ∠4 form a linear pair of angles:
- ∠1 + ∠4 = 180° (Linear pair angles are supplementary) - (Equation 2)
Since the right-hand sides of Equation 1 and Equation 2 are equal, we can equate the left-hand side of both equations and write it as:
- ∠1 + ∠4 = ∠5 + ∠4
By solving this equation, we find that ∠1 = ∠5, which forms a corresponding pair in the parallel lines.
Hence, we can deduce that one pair of corresponding angles is equal in the given figure, which can only occur if the two lines are parallel. Thus, the converse of the consecutive interior angle theorem is proven, which states that if a transversal intersects two lines such that a pair of consecutive interior angles are supplementary, then the two lines are parallel.
The Magic of Consecutive Interior Angles in a Parallelogram
In a parallelogram, the opposite sides are parallel. As a result, the consecutive interior angles of a parallelogram are always supplementary. Take a look at the parallelogram below for a clear example:
Image: Consecutive interior angles of a parallelogram
In this image, ∠A and ∠B, ∠B and ∠C, ∠C and ∠D, and ∠D and ∠A are consecutive interior angles. This relationship can be understood as follows:
- If we consider AB // CD and BC as the transversal, then ∠B + ∠C = 180°.
- If we consider AB // CD and AD as the transversal, then ∠A + ∠D = 180°.
- If we consider AD // BC and CD as the transversal, then ∠C + ∠D = 180°.
- If we consider AD // BC and AB as the transversal, then ∠A + ∠B = 180°.
Tips and Tricks for Consecutive Interior Angles
To sum it all up, here are some key points to remember about consecutive interior angles:
- Consecutive interior angles are non-adjacent angles located on the same side of a transversal.
- Two lines are parallel if and only if the consecutive interior angles are supplementary.
We hope this article has shed light on the power and significance of consecutive interior angles. By understanding the properties and theorems associated with these angles, you can unlock the secrets of parallel lines and their intricate relationships.
☛ Related Articles:
- Exterior Angle Theorem
- Pairs of Angles
- Supplementary Angles
- Intersecting and Non-Intersecting Lines
