Have you ever wondered about the angles that exist outside a polygon? Well, these angles are known as exterior angles, and they have some intriguing properties. In this article, we will delve into the realm of exterior angles and uncover their secrets. So, let's get started!
Understanding Exterior Angles of a Polygon
An exterior angle is formed when a side of a polygon intersects with the line extended from the next side. But what exactly are polygons? Polygons are flat shapes or figures that consist of at least three straight sides and three angles. The exterior angle is situated between the extended line and an adjacent side of the polygon.
One interesting observation is that the number of exterior angles in a polygon is equal to the number of sides it has. For instance, a pentagon has five sides and, consequently, five exterior angles. Additionally, the sum of the exterior angle and its adjacent interior angle is always 180° since they lie on a straight line. This concept is evident in shapes like squares and equilateral triangles.
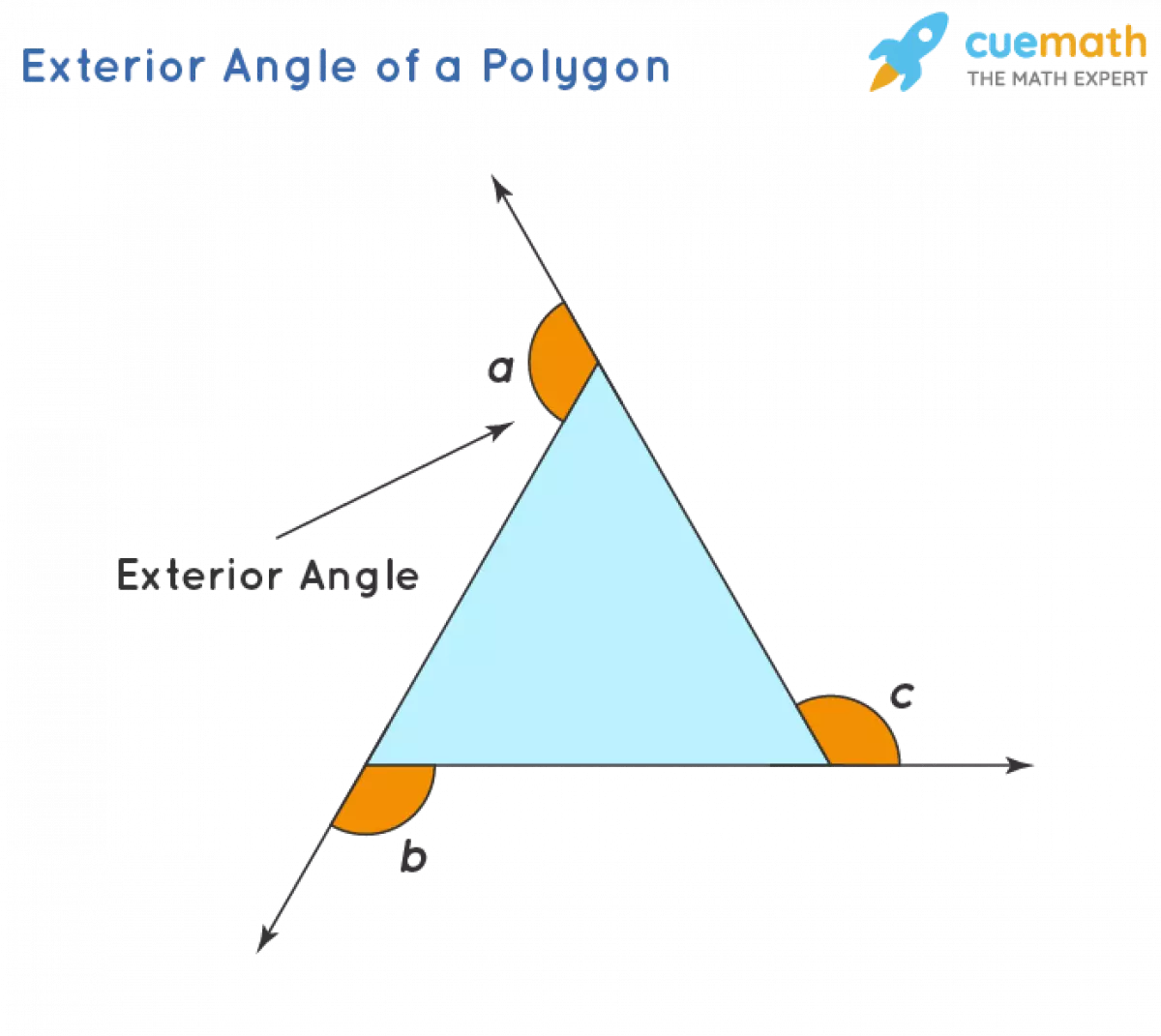Image source: Sanaulac.vn
Exploring Regular and Irregular Polygons
Both regular and irregular polygons possess exterior angles. A regular polygon is characterized by equal side lengths and angles, while an irregular polygon showcases sides and angles of varying measurements. The fascinating fact is that regardless of their regularity or irregularity, the sum of exterior angles in any polygon is always 360°.
Let's consider a regular hexagon as an example. This shape has six sides and six angles. If we assume that each exterior angle of the hexagon is 'k', we can imagine a circle starting at a specific point and making its way around the hexagon until it reaches the starting point again. The circle completes a full revolution, equivalent to 360°, by rotating through each vertex of the hexagon. Consequently, the sum of the exterior angles of the hexagon equals 360°, leading us to the conclusion that each exterior angle measures 60°.
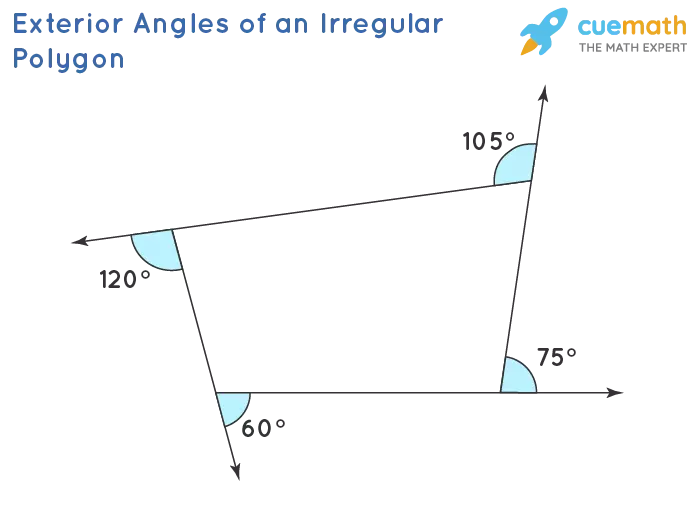Image source: Sanaulac.vn
In the case of irregular polygons, where sides and angles have different measurements, the sum of their exterior angles still amounts to 360°. Each exterior angle in an irregular polygon is equal to 180° minus its linear pair. As demonstrated by the figure below, the exterior angles add up to 360°.
Image source: Sanaulac.vn
Unveiling the Formula for Exterior Angles
For both regular and irregular polygons, we can derive a general formula to determine the measure of each exterior angle. It is important to note that the sum of each interior and exterior angle on a side of the polygon always equals 180° since they form a linear pair. Therefore, the formula for the exterior angle of a polygon can be expressed as 360° divided by the number of sides of the polygon.
An exterior angle of a polygon = 360° / Number of sides of the polygon.
Theorem: Sum of Exterior Angles in a Convex Polygon
If a polygon is convex, the sum of its exterior angles, considering one angle at each vertex, amounts to 360°.
Proof: Let's consider a polygon with 'n' number of sides or an 'n-gon'. The sum of its exterior angles is represented by 'N'. In any closed shape formed by a side and a vertex, the sum of the exterior angles is always equal to the sum of the linear pairs and the interior angles.
N = 180n - 180(n - 2) N = 180n - 180n + 360 N = 360.
Therefore, the sum of the exterior angles in an 'n-gon' polygon is always 360°.
Conclusion
In conclusion, exterior angles in polygons offer a fascinating glimpse into the world of geometry. Regardless of the regularity or irregularity of a polygon, the sum of its exterior angles remains constant at 360°. Understanding these angles and their properties can help us explore various aspects of polygonal shapes. So go ahead and delve into the mesmerizing realm of exterior angles in polygons!
Topics Related to Exterior Angles of a Polygon
- Definition of a Polygon
- Polygon Shape
- Regular Polygon
- Area of a Regular Polygon
- Interior Angles of a Polygon Calculator
- Exterior Angle Theorem
Remember, exploring the world of polygons is an exciting adventure that unveils the wonders of mathematics!
